Concept Learning

borrowed from : http://www.userwebs.pomona.edu/~jbm04747/courses/spring2003/cs151/lectures/VersionSpaces/VersionSpaces.html

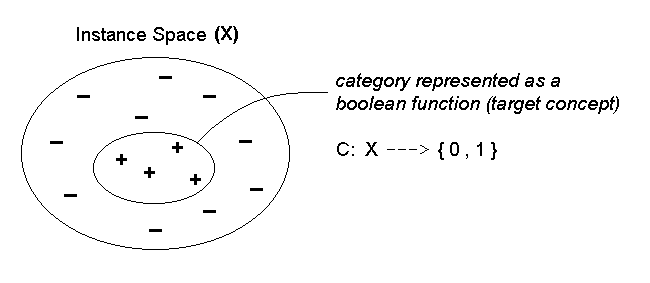
Examples:

"bird"
"car"
"Impressionist painting"
"catch-22 situation"
"days that are good for enjoying my favorite water sport"

A Concept Learning Task

Represent days (i.e., instances) using a set of attributes:

Sky: Sunny, Cloudy, Rainy
Temp: Warm, Cold
Humidity: Normal, High
Wind: Strong, Weak
Water: Warm, Cool
Forecast: Same, Change

Represent hypothesis as a conjunction of constraints on attribute values.

Possible attribute constraints:

single required value (e.g., Water = Warm)
any value is acceptable: ?
no value is acceptable: Ø

Example:

< Sky=Sunny, Temp=?, Humidity=High, Wind=?, Water=?, Forecast=? >

or just

< Sunny, ?, High, ?, ?, ? >

This is equivalent to a (restricted) logical expression:

Sky(Sunny) ^ Humidity(High)

Most general hypothesis: < ?, ?, ?, ?, ?, ? >

Most specific hypothesis: < Ø, Ø, Ø, Ø, Ø, Ø >

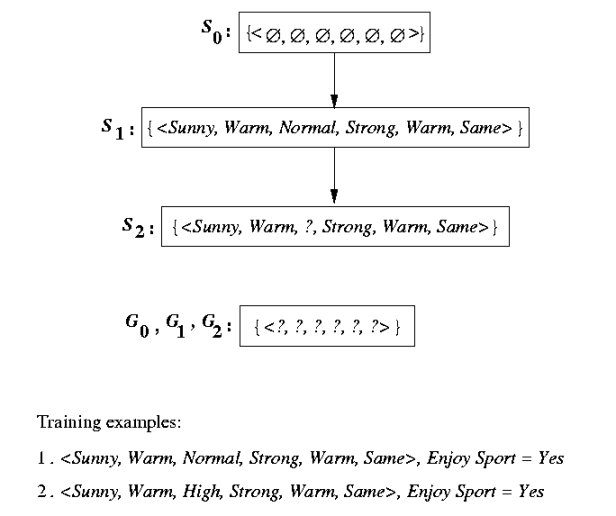
Positive and negative training examples for the concept EnjoySport:

Example	*Sky*	*Temp*	*Humidity*	*Wind*	*Water*	*Forecast*	*EnjoySport*
1	Sunny	Warm	Normal	Strong	Warm	Same	Yes
2	Sunny	Warm	High	Strong	Warm	Same	Yes
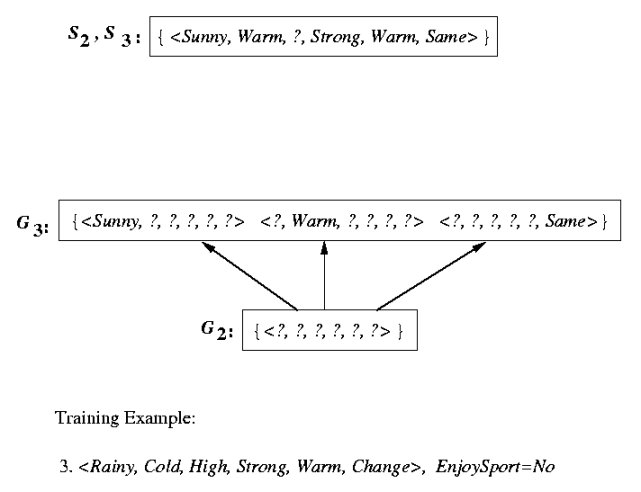
3	Rainy	Cold	High	Strong	Warm	Change	No
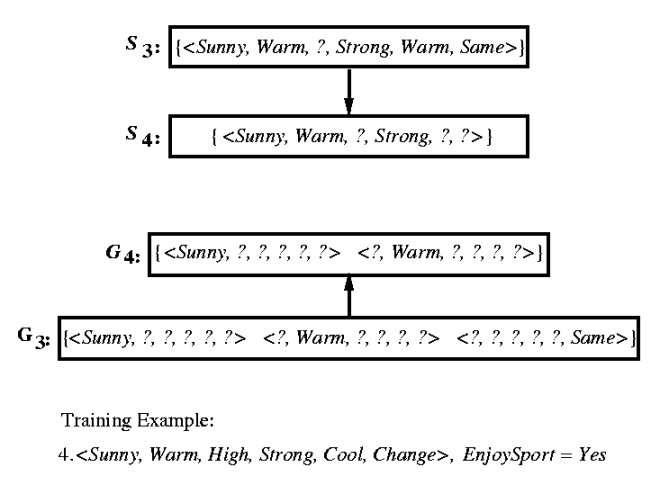
4	Sunny	Warm	High	Strong	Cool	Change	Yes

Task is to search hypothesis space for a hypothesis consistent with examples.

Inductive learning hypothesis:
    Any hypothesis found to approximate the target function well over
    a sufficiently large set of training examples will also approximate
    the target function well over other unobserved examples.

In this case, space is very small:

1 + ( 4 · 3 · 3 · 3 · 3 · 3 ) = 973

Ø + ( {Sunny, Cold, Rainy, ?} · { Warm, Cold, ? } · . . . )

Need a way of searching very large or infinite hypothesis spaces efficiently.

General-to-Specific Ordering

Hypothesis space H has a natural structure.

h1 = < Sunny, ?, ?, Strong, ?, ? >

h2 = < Sunny, ?, ?, ?, ?, ? >

h2 > h1 ("more general than or equal to")

> relation defines a partial-order on H.

h1 can be generalized to h2
h2 can be specialized to h1

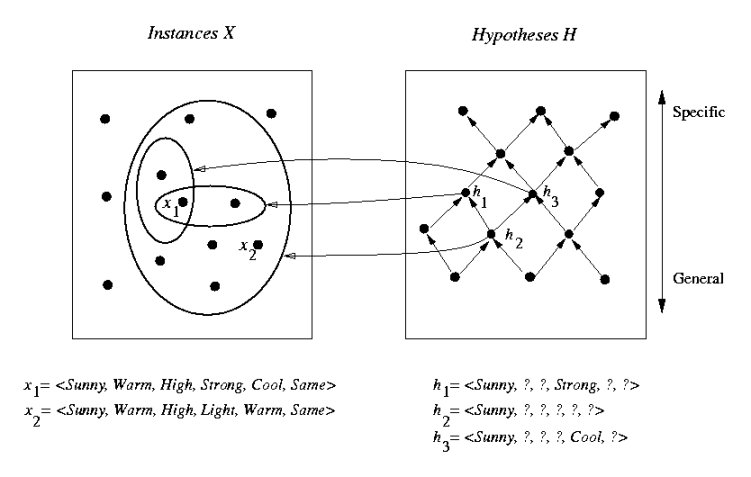
We can use this structure to search for a hypothesis consistent with the examples.

FIND-S Algorithm

Finds a maximally specific hypothesis.

    h <--most specific hypothesis in H
    for each positive training example x {
        for each attribute constraint a in h {
            if constraint a is not satisfied by x {
                replace a by next more general constraint that is satisfied by x
           }
        }
    }
    output hypothesis h

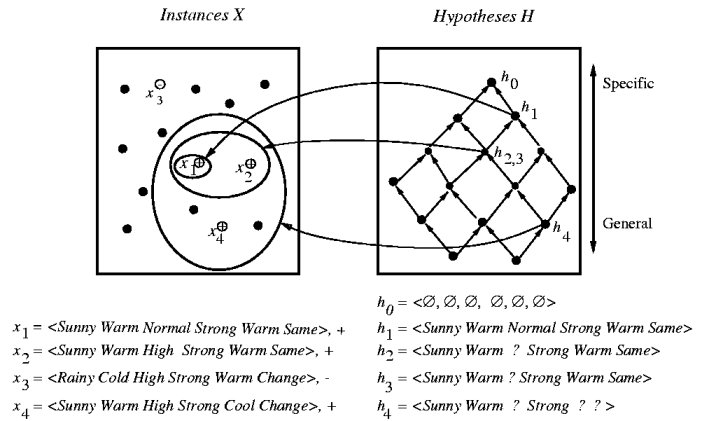
This method works, provided that:

H contains a hypothesis that describes the true target concept
No errors in training data
Hypotheses in H described as conjunctions of attribute constraints

Problems with FIND-S

Cannot determine if final h is the only hypothesis in H consistent with the data. There may be many other consistent hypotheses.

Why prefer most specific hypothesis? Why not most general consistent hypothesis (or one of intermediate generality)?

Fails if training data is noisy or inconsistent. Cannot detect inconsistent training data.

Cannot handle hypothesis spaces that may have several consistent maximally-specific hypotheses.

Not a problem with hypothesis representation used above, but may be if more general logical expressions (e.g., with disjunctions) are used. Must then use backtracking.

Current-Best-Hypothesis Search

generalization of FIND-S

uses backtracking and a more general hypothesis representation (arbitrary logical expressions, including disjunctions)

does not necessarily start from most-specific-possible hypothesis

Example:

*Sky*	*Temp*	*Humidity*	*Wind*	*Water*	*Forecast*	*EnjoySport*
Sunny	Warm	Normal	Strong	Cool	Change	Yes
Cloudy	Warm	Normal	Strong	Cool	Change	Yes
Rainy	Warm	Normal	Strong	Cool	Change	No

Not possible to find a consistent hypothesis using FIND-S.

FIND-S: < ?, Warm, Normal, Strong, Cool, Change > won't work

CBH: (Sky(Sunny) v Sky(Cloudy)) ^ Temp(Warm) ^ . . . ^ Forecast(Change)

Version Spaces

Idea: output the set of all hypotheses consistent with training data, rather than just one (of possibly many).

No need to explicitly enumerate all consistent hypotheses.

Take advantage of partial ordering of H.

The version space VS_H,D with respect to hypothesis space H and training examples D, is the subset of hypotheses from H consistent with the training examples D.

How to represent a version space?

One approach: Just list all the members.

List-Then-Eliminate Algorithm

    VS <-- a list of all hypotheses in H
    for each training example <x, f(x)> {
        remove from VS any hypothesis h such that h(x) != f(x)
    }
    output hypotheses in VS

Only works if H is finite and small (usually an unrealistic assumption).

Better representation for version spaces: Use 2 boundary sets:

S-set: least general (i.e., most specific) members of H
G-set: most general members of H

VS is the interval from S-set to G-set.

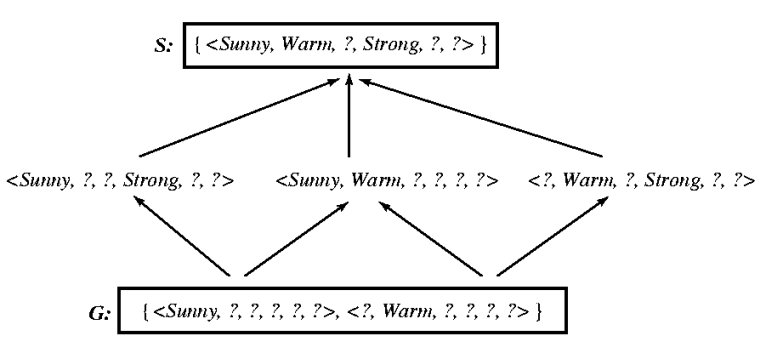
Total of 6 possible hypotheses consistent with EnjoySport training data
FIND-S only returns one of these (the most specific one)
Principle of least-commitment (like in partial-order planning algorithm)
All consistent hypotheses can be enumerated from S-set and G-set

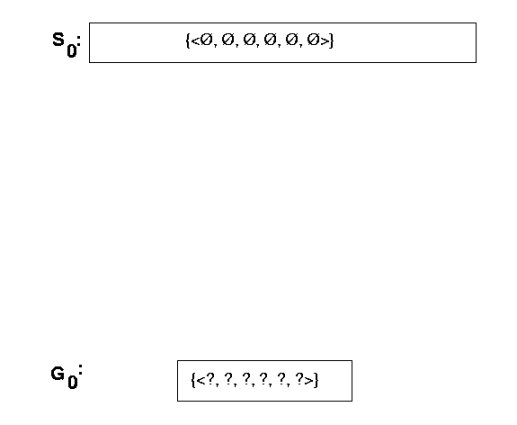
Version-Space Learning Algorithm

G <-- set of maximally general hypotheses in H (e.g., {<?,?,?,?,?,?>})
S <-- set of maximally specific hypotheses in H (e.g., {<Ø,Ø,Ø,Ø,Ø,Ø>})
for each training example e {
    if e is a positive example {
        remove from G any hypotheses inconsistent with e
        for each hypothesis s in S not consistent with e {
            1. remove s from S
            2. add to S all minimal generalizations h of s such that
                h is consistent with e, and some member of G is more general than h
            3. remove from S any hypothesis that is more general than another
                hypothesis in S
        }
    }
    if e is a negative example {
        remove from S any hypotheses inconsistent with e
        for each hypothesis g in G not consistent with e {
            1. remove g from G
            2. add to G all minimal specializations h of g such that
                h is consistent with e, and some member of S is more specific than h
            3. remove from G any hypothesis that is less general than another
                hypothesis in G
        }
    }
}

Example trace

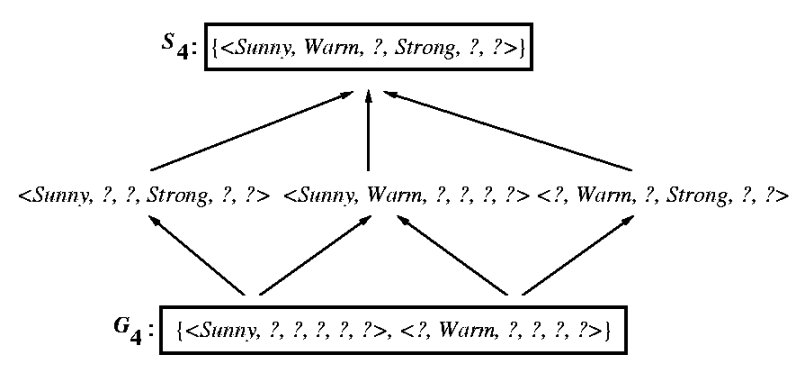
Behavior of Version-Space Learning

VS will converge to hypothesis that correctly describes target concept if:

no errors in training examples
H contains a hypothesis that correctly describes target concept

VS can be monitored to determine how "close" it is to the true target concept

if S and G converge to a single, identical hypothesis, then target concept has been learned exactly

VSL algorithm removes from VS every hypothesis inconsistent with each example, so the first incorrect/noisy example will eliminate the target concept from VS !

if S and G converge to the empty set, then no hypothesis in H is consistent with all training examples

VSL algorithm can thus detect inconsistencies in training data, assuming that the target concept is representable in H

How can Experiment-Generator module use current VS to suggest new problems to try?

Choose an instance that is classified as positive by half of the VS hypotheses, and as negative by the other half

Example: < Sunny, Warm, Normal, Light, Warm, Same > satisfies 3 out of 6 hypotheses in VS of earlier example

Partially-learned concepts (VS with > 1 hypothesis) can still be useful

if all hypotheses in VS agree on a particular novel instance, then classification must be correct

if an instance satisfies all hypotheses s in S, then instance must be positive

if an instance is rejected by all hypotheses g in G, then instance must be negative

above two tests can be done efficiently (no need to test all hypotheses in VS)

if hypotheses in VS give a mixture of positive and negative classifications, we can output a probability of correct classification (or use majority vote)

Example:

*New instance*	*Sky*	*Temp*	*Humidity*	*Wind*	*Water*	*Forecast*	*EnjoySport*
A	Sunny	Warm	Normal	Strong	Cool	Change	?
B	Rainy	Cold	Normal	Light	Warm	Same	?
C	Sunny	Warm	Normal	Light	Warm	Same	?
D	Sunny	Cold	Normal	Strong	Warm	Same	?

VS from earlier example says:

all hypotheses agree that A is positive
all hypotheses agree that B is negative
3 hypotheses say C is positive, 3 say negative (useful as a test to gain more info)
2 hypotheses say D is positive, 4 say negative (67% confidence that it is negative)