Extendible hashing for COSC 311

Why use it: Extendible hashing is particularly useful as an external hashing method, e.g., for databases. Data are frequently inserted, but you want good performance on insertion collisions by doubling and rehashing only a portion of the data structure (and not the entire space). Also, while regular internal hashing requires a large table with a lot of unused entries for good insertion and retrieval performance, extendible hashing's requirements for excess space is small.

Table and Buckets: The scheme comprises a hash table, which may be stored in main memory and one or more buckets stored on disk. The table size is always 2^d where d is called the global depth. Each table entry points to one bucket, i.e., contains a bucket pointer. A given bucket may have several table entries pointing to it.

Retrieval: To do retrieval, use of hashing is straightforward. The hash function is applied to some subset of the data (called the key), giving a result. Using the result's bit string, d contiguous bits give the index in the hash table. Follow the bucket pointer to the target bucket. If the low order bits are used, then this is equivalent to doing a h(key)%TABLESIZE. For the remainder of this write-up, however, I'll use the high order bits in order to simplify the drawing. (note, during the lecture on 4/4 I used the low-order bits)

Insertion: For insertion when the target bucket does not overflow, the process is also straightforward. Hash the key, take d bits to find the index, follow the hash table entry to the target bucket.

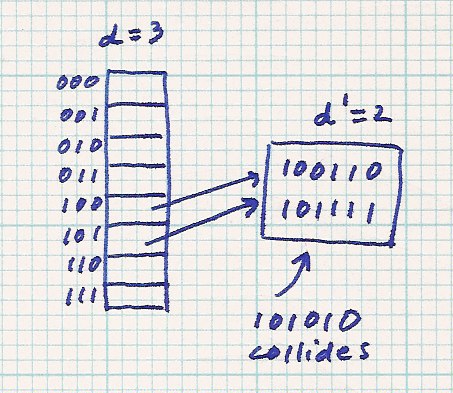
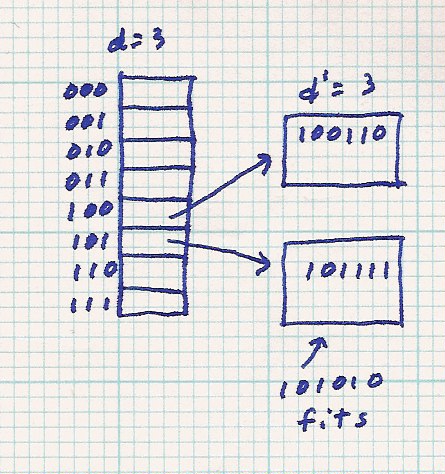
Insertion where d' < d: It is for insertion causing bucket overflow that things get interesting.

Each bucket has associated with it a local depth denoted d'. If d' for the overflowed bucket is less than d, the global depth, then a new bucket is allocated. Both the new bucket and the overflowed bucket are assigned local depth d'+1. The overflowed bucket contents are rehashed.

The rehashed data will go into the original bucket or the new bucket. This is a consequence of using d contiguous bits to hash. A bucket with depth d' has data that is distinguished from data in any other bucket using only d' bits. But the table makes use of d bits to find a bucket. For a hash value = b5b4b3b2b1b0, d=3, d'=2, bits b5b4b3 are used to find the index (and hence the target bucket), while bits b5b4 are the same for all elements of the target bucket.

Here is an example. Only the buckets and table entries of interest are shown. For this and future examples, we'll use bucket size = 2 to have lots of overflow.

Before split	After split

Notice the original bucket is reached through index 100 or 101. After it is split and rehashed, all the original data can only go to the buckets indexed by 100 or 101. The new data (101010) goes through index 101 to overflow the original bucket. After the split and rehash, the 101010 goes through index 101 to reach the new bucket. The rehashed data will never go through index 000 (for example).

As long as the data causes overflow on a bucket with d' < d, the process of splitting the bucket and rehashing can continue as necessary.

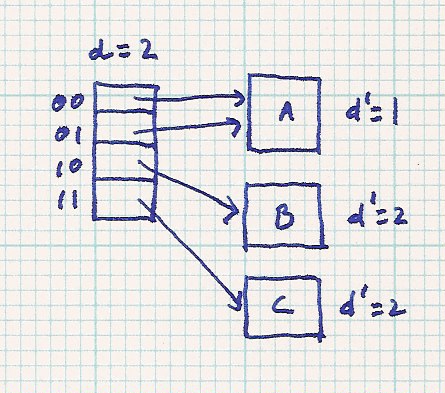
Insertion where d' = d: When d' = d, however, the overflowed bucket cannot be immediately split because there is no "give" in the hash table. Instead the hash table is doubled in size to 2^d+1 elements. Thus, the new global depth is d+1 (and now the local depth of the overflowed bucket is less than the global depth, and we already know what to do with that case). Each entry in the original hash table, indexed with b_kb_k-1. . .b₀ is duplicated into two entries: b_kb_k-1. . .b₀0 and b_kb_k-1. . .b₀1. The bucket pointer originally in b_kb_k-1. . .b₀ is copied to both of the new entries. Here is an example. Buckets are labelled with 'A', 'B', etc.

Before table doubling	After table doubling

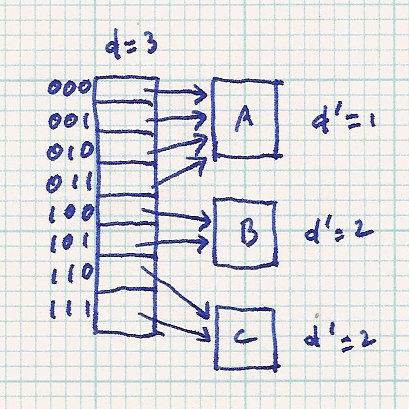So, before the table double, element 00 points to bucket A. After the table doubles, index 000 and 001 both point to bucket A. Before the table doubles, d=2. After the table doubles, d=3. Of course, all d' values are unchanged because buckets have not been split.

When there is overflow on a bucket with d' = d, the table must be doubled (the new d is now one greater than the d' of the overflowed bucket); then the overflowed bucket is split (cause the d' on the overflowed and the new buckets to be incremented by one); the overflowed bucket is rehashed; the new insertion element is retried.

Big demo: To demonstrate this, we'll hash the following data, only the hash value is binary is given, to an initial table size 1, d = 0 (2⁰ = 1). I'll only give the first 6 bits of the data. Recall that we're using the high order bits as indices.
000000, 010000, 110000, 001000, 111000, 100111, 111111, ...

Initial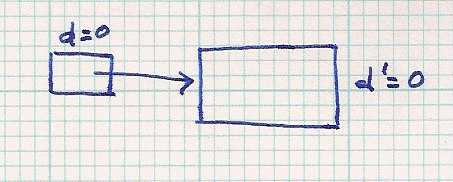
insert 000 000 - - > no problem
insert 010 000 - - > no problem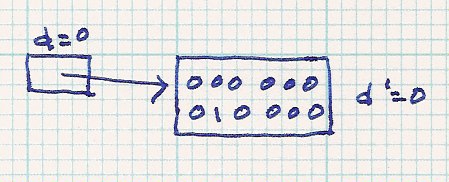
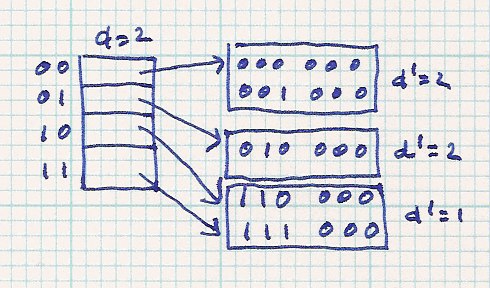
insert 110 000 - - > d > d', split bucket	split, rehash no problem now
insert 001 000 - - > d > d', split bucket	split, rehash no problem now
insert 111 000 - - > no problem
insert 100 111 - - > no problem
insert 111 111 - - > d=d', double table	split, rehash no problem now

Comments on programming

• How do you know the bucket size?
  The bucket size is calculated from the sector size of the hard disk, any overhead data (such as d') that goes with the bucket, and the record size. You put the maximum number of records that you can fit in the bucket in order to minimize hard disk access time (which is very time consuming).
  Suppose a data record occupies 220 bytes, d' is an int and thus occupies 4 bytes, and the sector size is 1024 bytes.
  

  p * 220 + 4 ≤ 1024
  p ≤ (1024 - 4) / 220
  p = floor(1020/220) = 4
  

  The bucket size is 4.
  
  
• How do you read and write buckets from the hard disk?
  The cleanest way is to define a class that matches how the data is laid out in the bucket. For a bucket with an int (for d') and 4 Records, you would define (in pseudocode):

  class Bucket {
     int depth;
     Record [4] data;
     }
  

  Then, allocate space in main memory for one Bucket and, using one read statement, read the desired bucket (file record) into the allocated space. The four different data records are stored in the data array. If you want to keep track of how many data records you have stored, then add that to the bucket definition, recalculate bucket size and change the definition of Bucket.
  
  Note the following important point! When you add a new data record (element) to a bucket, you do the following:

  Read in the original bucket to main memory,
  Add the new data record to an available location in the data array.
  Write the bucket to the original bucket location (watch out! the file cursor usually advanced 
  when you did the read).
  

  Note also that when you are writing a completely new bucket, it goes to the end of the file.
  
  
• Is there anything in an empty bucket?
  Absolutely yes! An empty bucket occupies space (the size of a bucket) on the hard disk. Fill it with null or 0 or any other data that indicates empty to you. In main memory, an empty bucket has allocated space, even though it contains no meaningful data yet.
  
  
• It doesn't make sense to reserve an empty bucket when I do a bucket split. I may not be putting anything in an empty bucket.
  OK -- you're trading off ease of programming with occupying space. The program will be a little easier to write if you waste space on the occasional empty bucket, but if that really bugs you, then don't do that. Instead, handle the split and rehash in the following way:

  Read the original bucket into memory.
  Save the file address of the original bucket to tmp.
  In the hash table, change the two bucket pointers that point to the original bucket to null.
  Allocate space for two new buckets in main memory.
  Rehash all data records in the original bucket to the corresponding new bucket (memory ops only).
  After all data records are rehashed, 
     if there is only one bucket in main memory used, then store tmp to the proper hash table location
        and write the bucket to that location (overwriting the original bucket).
     else (both main memory buckets are used in the rehashing), then
     			overwrite one bucket as above (set hash table entry correctly)
     			write the second bucket to the end of the file and set hash table entry.
  

Version 1.0