Given a set of n values, a0, a1, ... an-1
and an associative binary operator ⊕,
reduction computes a0 ⊕ a1 ⊕ . . . ⊕ an-1
Parallel summation is an example of reduction

A[]using floor(n/2) steps.
spawn (P0, P1, ... Pfloor(n/2)-1)
forall Pi where 0 ≤ i ≤ floor(n/2)-1 {
for (j=0; j ≤ ceil(log n); j++) {
if (( i % 2j == 0) && (2 i + 2j < n)) {
A[2 * i] = A[2 * i] + A[2 * i + 2j ]
} //if
} // for j
} // forall
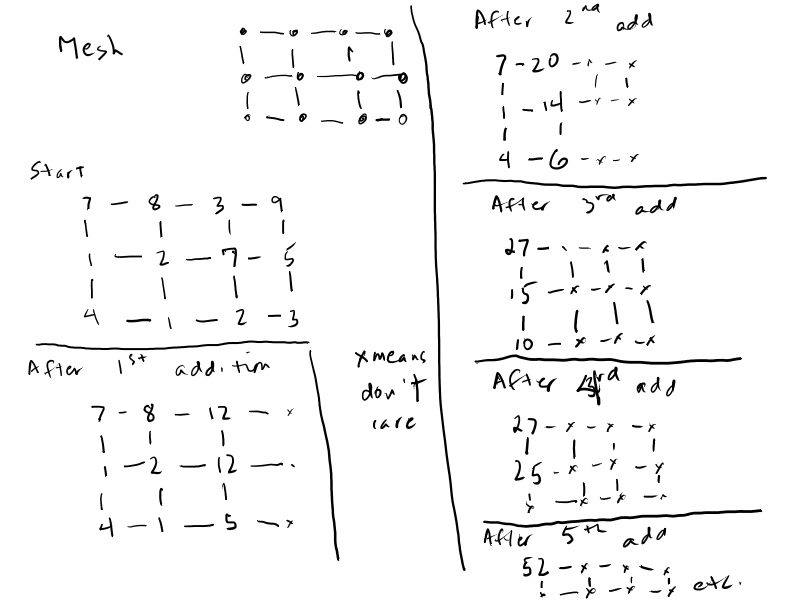
n X n
Each processor Pij finds sum of local values
// accumulate intermediate results into column 0
for (i = n - 1 i ≥ 1; i--) {
forall Pj,i where (1 ≤ j ≤ l) {
// processing elements in col i active
tmp = east(sum); // local tmp gets sum value from east neighbor
sum = sum + tmp;
} // end forall
} // end for i
for (i= n - 1; i ≥ 1; i--) do {
forall Pi, 1 do {
// a single element is active
tmp = south(sum) // get sum value from south neighbor
} // end forall
} // end for i b
Sum is contained in P0,0
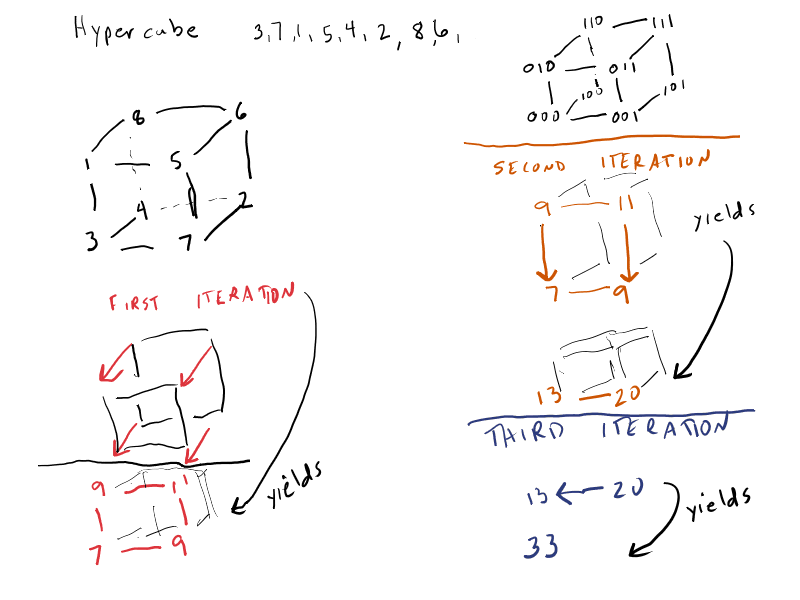
# elements to add: n
# processing units: p
local array of elements: localValue[1 ... ceil(n/p)]
begin
forall Pi where 0 ≤ i ≤ p-1 do {
if (i < n%p) then localSetSize = ceil( n/p );
else localSetSize = floor( n/p );
}
sum = 0;
} // forall
for (j = 1; j ≤ ceil(n/p); j++) do {
forall Pi where 0 ≤ i ≤ p-1 do {
if (localSetSize ≥ j) then sum += localValue[j];
} // forall
} // for
for (j= log p - 1; j ≥ 0; j-- ) {
forall Pi where 0 ≤ i ≤ p-1 {
if (i < 2j) {
tmp = get(sum from Pi+2j );
sum += tmp;
} // if
} // forall
} // for
end // begin
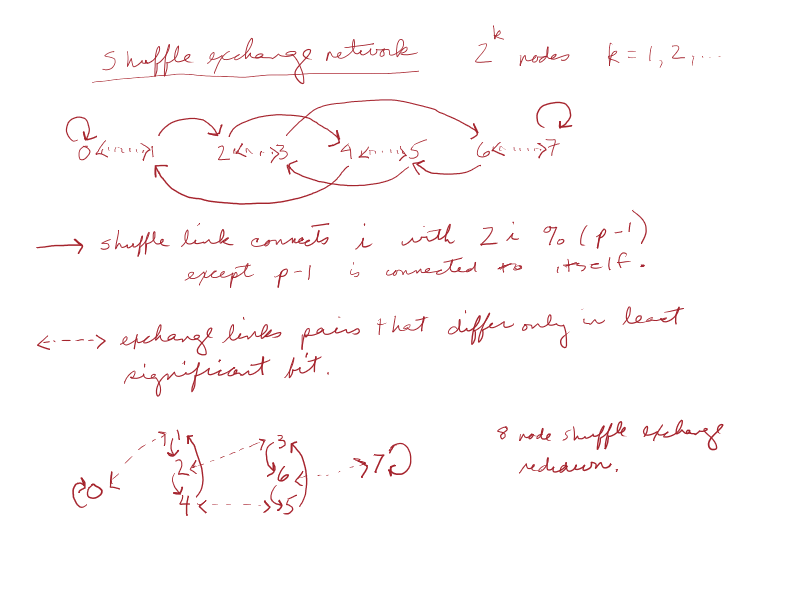
# elements to add: n
# processing units: p
local array of elements: localValue[1, ... ceil(n/p)]
local size of dataset: localSetSize
begin
forall Pi where (0 ≤ i ≤ p-1) do {
if (i < n%p) localSetSize = ceil(n/p);
else localSetSize = floor(n/p);
sum = 0;
} //end forall
for (j = 1; j ≤ ceil(n/p); j++) {
forall Pi where (0 ≤ i ≤ p-2) {
if (localSetSize ≥ j) sum += locaalValue[j];
} // end forall
for (j = 0; j ≤ log p - 1; j++ ) {
forall Pi where 0 ≤ i ≤ p-1) {
shuffle(sum) = sum; //send local sum to shuffle connected node's sum
exchange(tmp) = sum; // send local sum to exchange-connected node's tmp
sum += tmp;
} // end forall
} // end for j