CS315 Lab 5: Illumination 2

This is a modified version of a lab written by Alex Clarke at the University of Regina Department of Computer Science for their course, CS315. Any difficulties with the lab are no doubt due to my modifications, not to Alex's original!

Highlights of this lab:

1. The Blinn Phong equation revisited
2. Hemisphere lighting
3. Distance and Positional Lights

Assignment:

• Isolate the Blinn-Phong Specular Lighting code from example 1's shader and add it to example 2's shader
• Create and name a material
• Light it with a pleasing light

To follow along with the lab as you read it, you should first download Lab5E.zip

Lab Notes

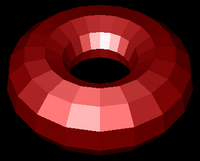
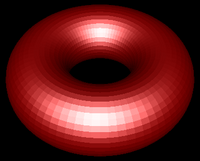
In last week's lab you saw these pictures. They show a full implementation of the Blinn-Phong reflection equation being applied in three different ways. The first is flat shading - one color is used for one whole primitive (triangle). The second is Gouraud shading - reflection is only calculated at the vertices, and colors are interpolated. The last is Phong shading - the full lighting equation is performed per fragment in the fragment shader. This week you will see results that look like all three columns, but you will always be doing Gouraud shading. You will add the Blinn-Phong specular component to a vertex shader, which produces the whitish highlight you see. The smoothness or flatness you will observe will be created entirely in the model - either by using the same normal for all vertices of a primitive (flat-like results) or high resolution meshes (Phong-like results).

Flat Shading	Gouraud Shading	Phong Shading
Figure 3:Torus at different resolutions lit with Blinn-Phong reflection and shaded with different shading models.

A. Blinn-Phong Equation Revisited

When you start to work with lighting, you move beyond color to normals, material properties and light properties. Normals describe what direction a surface is facing at a particular point. Material properties describe of what things are made of — or at least what they appear to be made of — by describing how they reflect light. Light properties describe the type and colour of the light interacting with the materials in the scene. Lights and materials can interact in many different ways. Describing these many different ways is one reason shaders are so important to modern 3D graphics APIs.

One common lighting model that relates geometry, materials and lights is the Blinn-Phong reflection model. It breaks lighting up into three simplified reflection components: diffuse, specular and ambient reflection. In this week's lab we will focus on specular reflection. The other two are left here for your reference.

Specular Reflection

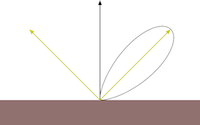
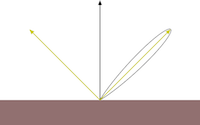
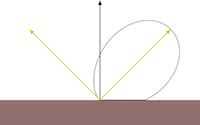
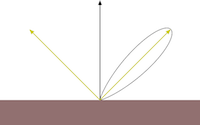
Specular reflection represents the shine that you see on very smooth or polished surfaces. Phong specular reflection takes into account both the angle between your eye and the direction the light would be reflected. As your eye approaches the direction of reflection, the apparent brightness increases. It assumes that light will be scattered toward the mirror reflection direction. A special shininess parameter (labelled α in the textbook, but s, here) is used to control how tight this scattering is. The Blinn-Phong specular reflection is very similar to Phong, but it fixes some technical shortcomings having to do with backscatter (compare the curves you see if figure 5). Instead of using the reflection vector it uses a vector that is halfway between the light and the eye. This vector is then compared to the normal.

The Blinn-Phong specular component is calculated by these equations:

h = (e+l)/|(e+l)|
I_s = m_s L_s (h · n)^s

Where:

• I_s is the intensity of specular reflection
• m_s is the material's specular color
• L_s is the light's specular color
• l is the normalized direction to the light
• e is the normalized direction to the eye
• n is the surface normal
• s is the exponent that controls shininess.

	Specular exponent
	1	10	100
Phong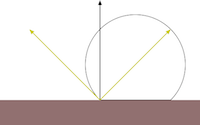
Blinn-Phong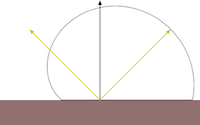
Figure 5: Phong vs Blinn-Phong With Varying Shininess Values. Both the Phong and Blinn-Phong reflectance functions cause a highlight to appear around the direction of reflection. Blinn-Phong has a fix that allows a near-diffuse disctribution at low shininess. Notice that at shininess 1 the Phong highlight would be invisible past 90° from the reflection direction, but Blinn-Phong is visible well past that point. Blinn-Phong also appears slightly more diffuse at all shininess values than Phong.

Figure 6: Blinn-Phong at Varying Angles.

Diffuse Reflection

Diffuse reflection is the more or less uniform scattering of light that you see in matte or non-shiny materials, like paper. The intensity that you see depends solely on the position of the light and the direction the surface is facing. The Blinn-Phong model calculates it using the Lambertian reflectance equation:

I_d = m_d L_d (l · n)

Where:

• I_d is the intensity of diffuse reflection
• m_d is the material's diffuse color
• L_d is the light's diffuse color
• l is the normalized direction to the light
• n is the surface normal

The dot product between l and n corresponds to the cosine of the angle between the two vectors. If they are the same, then the dot product is 1 and the diffuse reflection is brightest. As the angle increases toward 90° the dot product approaches 0, and the diffuse reflection gets dimmer. This change resembles the how a fixed width of light spreads out over a greater area when it hits a surface at different angles, as illustrated in Figure 4.

Figure 4: The same width of light covers a larger area as its angle to the surface normal increases.

Ambient Reflection

Even if the light does not reach a point on the surface directly, it may reach it by reflecting off of other surfaces in the scene. Rather than compute all the complex interreflections, we approximate this with ambient reflection. The ambient reflection is a simple product of the ambient colors of both the light and material. Direction does not factor in. The ambient reflectance equation is then:

I_a = m_a L_a

Where:

• I_a is the intensity of ambient reflection
• m_a is the material's ambient color
• L_a is the light's ambient color

Putting Things Together

I = I_s + I_d + I_a

//diffuse and ambient multi-light shader

//inputs
attribute vec4 vPosition;
attribute vec3 vNormal;

//outputs
varying vec4 color;

//structs
struct _light
{
    vec4 diffuse;
    vec4 ambient;
    vec4 specular;
    vec4 position;
};

struct _material
{
    vec4 diffuse;
    vec4 ambient;
    vec4 specular;
    float shininess;
};

//constants
const int n = 1; // number of lights

//uniforms
uniform mat4 p;     // perspective matrix
uniform mat4 mv;    // modelview matrix
uniform bool lighting;  // to enable and disable lighting
uniform vec4 uColor;    // colour to use when lighting is disabled
uniform _light light[n]; // properties for the n lights
uniform _material material; // material properties

//globals
vec4 mvPosition; // unprojected vertex position
vec3 N; // fixed surface normal

//prototypes
vec4 lightCalc(in _light light);

void main() 
{
  //Transform the point
  mvPosition = mv*vPosition;  //mvPosition is used often
  gl_Position = p*mvPosition; 

  if (lighting == false) 
  {
	color = uColor;
  }
  else
  {
    //Make sure the normal is actually unit length, 
    //and isolate the important coordinates
    N = normalize((mv*vec4(vNormal,0.0)).xyz);
    
    //Combine colors from all lights
    color.rgb = vec3(0,0,0);
    for (int i = 0; i < n; i++)
    {
        color += lightCalc(light[i]);
    }
    color.a = 1.0; //Override alpha from light calculations
  }
}

vec4 lightCalc(in _light light)
{
  //Set up light direction for positional lights
  vec3 L;
  
  //If the light position is a vector, use that as the direction
  if (light.position.w == 0.0) 
    L = normalize(light.position.xyz);
  //Otherwise, the direction is a vector from the current vertex to the light
  else
    L = normalize(light.position.xyz - mvPosition.xyz);

  //Set up eye vector
  vec3 E = -normalize(mvPosition.xyz);

  //Set up Blinn half vector
  vec3 H = normalize(L+E); 

  //Calculate specular coefficient
  float Ks = pow(max(dot(N, H),0.0), material.shininess);
  
  //Calculate diffuse coefficient
  float Kd = max(dot(L,N), 0.0);

  //Calculate colour for this light
  vec4 color =  Ks * material.specular * light.specular
  			   + Kd * material.diffuse * light.diffuse
               + material.ambient * light.ambient;
               
  return color;
}

Appropriate changes should be made to get and set the specular color and shininess uniforms. The process is similar to what you observed with diffuse and ambient lighting.

Specifying Material Properties

Classic OpenGL has five material properties affect a material's illumination. They are introduced in the Blinn-Phong model section and implemented in the shaders in lab demo 2. They are explained below.

Diffuse and ambient properties:

The diffuse and ambient reflective material properties are a type of reflective effect that is independent of the viewpoint. Diffuse lighting describes how an object reflects a light that is shining on the object. That is, it is how the surface diffuses a direct light source. Ambient lighting describes how a surface reflects the ambient light available. The ambient light is the indirect lighting that is in a scene: the amount of light that is coming from all directions so that all surfaces are equally illuminated by it. Both properties are usually set to the similar colors, though the ambient color is usually scaled down or darker than the diffuse color.

Specular and shininess properties:

The specular and the shininess properties of the surface describe reflective effects that are affected by the position of the viewpoint. Specular light is reflected light from a surface that produces the reflective highlights in a surface. The shininess is a value that describes how focused the reflective properties are.

Emissive property:

Emissive light is the light that an object gives off by itself. Objects that represent a light source are typically the only objects that you give an emissive value. Lamps, fires, and lightning are all objects that give off their own light.

Choosing the Material Properties for an Object

The steps are as follows:

1. Decide on the diffuse and ambient colors;
2. Decide on the shininess of the object.
3. Decide whether the object is giving off light. If it is, assign it the emissive properties

Seeing the effects of varying material properties may help you select the ones you want.

In this week's first demo, L5-1, specular, diffuse and ambient material properties have been implemented. They have been declared for you globally, given default values and sent to the shader. The program provides convenient color pickers to allow you to select different specular and diffuse/ambient colors interactively. It also provides sliders to rotate the light about the Y-axis and change the shininess value. You should take some time to get familiar with the effects of the different properties.

Click here to view demo on its own.

Hemisphere Lighting

Specular lighting adds a lot to diffuse and ambient lighting as taught in the textbook. The ambient components are a hack to simulate global illumination, and they do a pretty poor job. Unless you use textures, there's no detail to be seen in ambient light - only a flat silhouette. Hemisphere lighting is a better looking hack that extends the light all around the object. It uses two colors of light, but each considered to be in opposite hemispheres shining toward the object. Toward the middle, the two colors blend smoothly. These colors are intended to represent the sky and the ground, but many implementations allow you to specify the direction of the north pole, or top hemisphere, so it becomes simple to specify directional, two color global illumination.

This picture illustrates the intent:

Figure 5: Hemisphere lighting's concept. Light falls on the object from two opposite hemispheres and blends across the object.

Downward facing normals are lit entierly by the bottom hemisphere. Upward facing normals are lit entirely by the upper hemisphere. Angled normals are linearly blended (or "lerped") between the two, based on their angle to the "north pole" or top direction.

The proper equation for this is:

Color = a · TopColor + (1 - a) · BottomColor

Where:

a = 1.0 - (0.5 · sin(Θ)) for Θ ≤ 90°
a = (0.5 · sin(Θ)) for Θ > 90°

This can be simplified without too much error to:

a = 0.5 + (0.5 · cos(Θ))

Which replaces an expensive sin() with a cos() and saves a branch instruction. Remember that in WebGL shader programs both paths through a branch are always executed, so the elimination of the conditional can potential double the speed of this block of code. Since this method of global illumination is already approximate, the error is mostly harmless. Here are the two curves overlaid on each other:

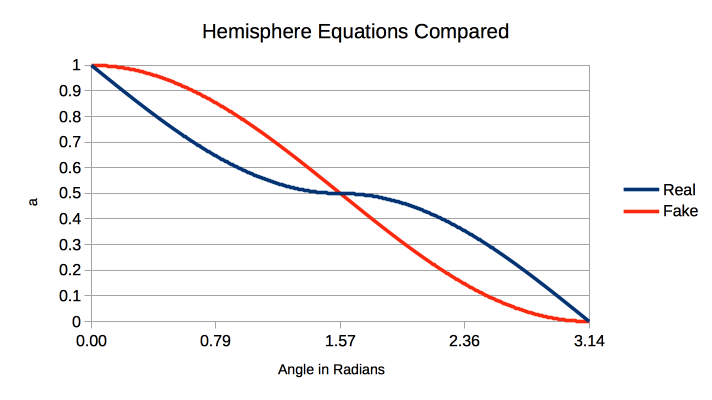Figure 6: Comparison of real vs. fake a calculation for hemisphere lighting.

The following shader implements hemisphere lighting. You will find it in L5-2.html:

//hemisphere lighting shader with optional diffuse lighting path

//inputs
attribute vec4 vPosition;
attribute vec3 vNormal;

//outputs
varying vec4 color;

//structs
struct _light
{
    vec4 top;
    vec4 bottom;
    vec4 direction;
    bool hemisphere;  // to switch between hemisphere and directional lighting
};

struct _material
{
    vec4 diffuse;
};

//uniforms
uniform mat4 p;     // perspective matrix
uniform mat4 mv;    // modelview matrix


uniform _material material; // material properties
uniform _light light;		// light properties

//globals
vec4 mvPosition; // unprojected vertex position
vec3 N; // fixed surface normal

void main() 
{
  //Transform the point
  mvPosition = mv*vPosition;  //mvPosition is used often
  gl_Position = p*mvPosition; 

  //Make sure the normal is actually unit length, 
  //and isolate the important coordinates
  N = normalize((mv*vec4(vNormal,0.0)).xyz);
    
  //Clean up light direction
  vec3 L;
  L = normalize(light.direction.xyz);
  
  //Calculate cosine of angle between light direction and normal
  float costheta = dot(L,N);

  //Calculate appropriate lighting colour
  if (light.hemisphere == true) //hemisphere technique
  {
  	float a = 0.5+(0.5*costheta);
  	color = a * light.top * material.diffuse
  	      + (1.0-a)* light.bottom * material.diffuse;
  }
  else	//lambertian technique with pseudo-ambient
  {
  	float Kd = max(costheta, 0.0);
  	color = Kd * material.diffuse * light.top
               + material.diffuse * light.bottom;
  }

  color.a = 1.0; //Override alpha from light calculations
}

And here is Lab 5 Demo 2, L5-2, for you to experiment with:

Observe how much detail you can make out in the shadows with Hemisphere Lighting as compared with Lambertian Directional Lighting. Notice, also, that the latter is brighter - this is because the ambient and diffuse colors are added rather than linearly blended.

C. Distance and Positional Lights

In the real world a point light source, or positional light, will have less power to light an object the farther the two are apart. This is called attenuation. Because the light spreads out in an ever increasing sphere, the intensity of the light decreases in inverse proportion to the square of the distance. Classic OpenGL has three parameters to calculate the attenuation factor: constant, linear, and quadratic attenuation. These three factors are used as shown in this equation:

float attenuation = 1.0
if (/* light is positional */)
{
   float lightDistance = length(light.position.xyz - mvPosition.xyz);
   attenuation = 1.0/(constant + linear * lightDistance + quadratic * lightDistance^2);
}

In the above code, constant could be any positive float. Linear and quadratic are both factors in the range [0.0-1.0] indicating to what extent the attenuation involves linear and quadratic components. This calculation is applied separately to the entire color of each light - you multiply that light's color by the attenuation, something like this

// where color is the color result for one light
// and attenuation is 1 for directional lights
color = attenuation * color;

• Constant attenuation is easiest to work with for beginners, and it gives an easy way for you to dim the lights - just crank up the constant attenuation. Set linear and quadratic to be 0.0 so that attenuation is = 1.0/constant. Thus, if constant is 2.0, attenuation will be 0.5, and color will be half of what it would have been.
• Linear attenuation sometimes gives more natural results if you are not doing HDR tone mapping or some other color correction. Set linear to be 1.0, quadratic to be 0.0, and constant to be 0. Now attenuation will become smaller, linearly, as the distance between the light and the object grows.
• Quadratic attenuation is the physically correct term to use, but it causes extreme light differences at short distances, so it is often avoided. Set linear to be 0.0, quadratic to be 1.0, and constant to be 0. Now attenuation will become smaller, quadratically, as the distance between the light and the object grows. Thus the color resulting from the interaction between the light an the object will decrease rapidly as the distance between them grows.

Attenuation is not implemented in the shaders in this week's lab. This is left for you to do as an exercise.

Assignment

Before you begin, be sure you are using the Common folder from Lab5E.zip. This lab adds two important libraries - Apple's j3di.js, which provides an OBJ file loader, and East Desire's jscolor.js which provides the color picker you see in the demos. They are in this folder for your convenience.

Remember that for your program to be able to load OBJ files (such as the Batman model in this demo) from your file system you may have to start Chrome like this on a Mac:

open /Applications/Google\ Chrome.app --args --allow-file-access-from-files

Alternatively, you can run your program with Firefox.

Goals:

• Understand the two new lighting concepts introduced in this lab
• In the specular shader, replace per-light source ambient illumination with global hemisphere illumination.
• Add distance-based attenuation calculations to the specular shader.
• Play with light and material properties to produce a pleasing result.

Instructions

1. Study how the specular shader in the lab notes and example L5-1.html/L5-1.js works.
2. Study how the simplified global hemisphere shader in the lab notes and example L5-2.html/L5-2.js works.
3. (Note that L5E.html and L5E.js are a slightly modified version of L5-1.)
4. Move the global hemisphere shading code from L5-2.html's vertex shader to the one in L5E.html.
   • Bring over the light.top, light.bottom and light.direction uniforms as global.top, global.bottom and global.direction. To do this, introduce a new global variable with a top, bottom, and direction field.
     • Notice that hemispherical calculations are supposed to go in main, not the lightCalc function. This is because there is only one global hemisphere light, but there can be many positional or directional lights.
     • Modify lightCalc and main so that the per-light ambient component in the original L5E code is replaced with the global hemisphere lighting.
   • Set up controls for the colors and direction of the light.
   • Choose your own background for the canvas.
   • The necessary code is in L5-2.html and L5-2.js. Look for the style on the canvas element in the .html file, and be sure to enable blending and a clear color of (0,0,0,0) as is done in the .js file's init function.
5. Make the appropriate changes to L5E.js to use the modified shader and controls.
6. Experiment with global light properties until you find a combination that fits your background. You might want to dim or disable the positional light while you do this.
7. Experiment with material properties until you find a material you like. Set your material as the default and name it - your lab instructor can show you examples of materials they like in the L5-1 demo to help you get some ideas. Be sure to set specular color and shininess.
8. Implement the attenuation calculation described in the lab notes, including constant, linear and quadratic factors.
   • Choose default settings for your factors that reasonably show that as you move the positional light with the A S D and W keys (AD for left and right on x-axis, SW for positive and negative along z-axis), the light brightens and dims.
   • The C key should set the attenuation calculation to be constant, the L key to linear, and the Q key to quadratic.

 /10

Deliverables

• Submit to Canvas a zip file containing a copy of your Lab5 and Common folders.
• The Lab5 folder should contain html and javascript files with complete solutions to the exercises. Please write the name of your material from step 7 with a description at the top of your HTML document.
• Please either put your solution into L5E.html and L5E.js or into files clearly marked as belonging to the exercise.

References

• j3di.js on github
• j3di.js sample on the official Khronos WebGL Wiki Tutorial
• jscolor.js Javascript Color Picker
• The Hemisphere Lighting concept and math are from "OpenGL Programming Guide 8th Ed.: The Official Guide to Learning OpenGL Version 4.3" by Dave Shreiner, Graham Sellers and John Kessenich, Hemisphere Lighting section