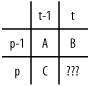
In a previous lecture we examined how BLAST can be used to search for matches of a given sequence of bases or amino acids against large databanks of other such sequences. Now we're going to look at one way to make such determinations (though not the way BLAST does--it uses a much more efficient algorithm). What makes this problem difficult is that we are looking only for approximate matches. We want to find the best approximate matches from among the elements of our databank.
The first problem is to define what we mean by "approximate". Here we quantify our "approximation degree" with the edit distance between a given pattern string and a text string. We suppose there are only three possible editing operations: substitution, deletion and insertion. The edit distance between any two strings is the minimum number of these operations that must be applied to make the two strings equivalent. Suppose the two strings are: sumptuous and virtuous. The edit distance of these two strings is 4 because we can "convert" sumptuous into virtuous via this sequence of operations:
There are many other sequences of operations that could be applied to both strings to obtain their equivalence, but four is the fewest that is required.
The purpose of this paper is to discuss how we can write a program that identifies the substring in a text that has the smallest edit distance to our pattern. To identify the substring, our algorithm builds a distance matrix, which can be used to determine the edit distance between the pattern and all substrings in the text. Below is the distance matrix that our algorithm generates for a pattern of EIQADEVRL and a text of SVLQDRSMPHQEILAADEVLQESEMRQQDMISHDE. The leftmost column shows the pattern, and the top row shows the text. The matrix entry at row i, column j concerns the i-character prefix of the pattern and the i-character substring that ends at the jth character in the target text. For example, the red, underlined 1 (row 3, column 13) in the table corresponds to the edit distance between the 3-character prefix of the pattern ("EIQ") and the 3-character substring ending at the 13th character in the target ("QEI"). This seems like it's not quite right, but in this case we could have inserted a 'Q' at the begining of the pattern, and then the 3-character prefix of the pattern would match this substring.
PATTERN:
EIQADEVRL
TEXT:
S V L Q D R S M P H Q E I L A A D E V L Q E S E M R Q Q D M I S H D E
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
E 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 0
I 2 2 2 2 2 2 2 2 2 2 2 2 1 0 1 2 2 2 1 1 2 2 1 1 1 1 2 2 2 2 2 1 2 2 2 1
Q 3 3 3 3 2 3 3 3 3 3 3 2 2 1 1 2 3 3 2 2 2 2 2 2 2 2 2 2 2 3 3 2 2 3 3 2
A 4 4 4 4 3 3 4 4 4 4 4 3 3 2 2 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 3 3 3 4 3
D 5 5 5 5 4 3 4 5 5 5 5 4 4 3 3 2 2 2 3 4 4 4 4 4 4 4 4 4 4 3 4 4 4 4 3 4
E 6 6 6 6 5 4 4 5 6 6 6 5 4 4 4 3 3 3 2 3 4 5 4 5 4 5 5 5 5 4 4 5 5 5 4 3
V 7 7 6 7 6 5 5 5 6 7 7 6 5 5 5 4 4 4 3 2 3 4 5 5 5 5 6 6 6 5 5 5 6 6 5 4
R 8 8 7 7 7 6 5 6 6 7 8 7 6 6 6 5 5 5 4 3 3 4 5 6 6 6 5 6 7 6 6 6 6 7 6 5
L 9 9 8 7 8 7 6 6 7 7 8 8 7 7 6 6 6 6 5 4 3 4 5 6 7 7 6 6 7 7 7 7 7 7 7 6
The best match for the pattern EIQADEVRL
has an edit distance of 3
and appears in the text ending at location 20
We will use an algorithm to solve our problem that makes use of a technique called dynamic programming. Dynamic programming is means of encoding a recursive solution to a problem by using iteration in place of the recursion. Suppose that our matching operation will be accomplished by right-to-left scans on the pattern. Consider the element at [p][t] (row p, column t, which we'll label "???"). The algorithm calculates this value from the values at [p-1][t-1] (which we'll call A), [p][t-1] (which we'll call B) and [p-1][t] (which we'll call C). Thus, the algorithm must calculate those values before it can calculate [p][t]. These values are shown in the diagram below.
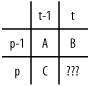
In an exact matching algorithm there is exactly one action that can be taken if a mismatch is found--we shift the pattern to compare it against a different substring in the text. But in this approximate matching, there are four possibilities: shift the pattern, replace a character, delete a character, or insert a character. We start with the first two possible actions. Case A supposes we've found an approximate match of the p-1 character prefix of the pattern against the substring of the text of the same length ending at position t-1. This match required A edits. Now suppose we extend the prefix by one, and extend the substring by one. There are two possibilities: the additional character of the pattern matches that of the text, or it doesn't. If it matches, then 0 additional edits are required to extend the match. If they are different, then we'll need to substitute for either the last character of the pattern or of the text, so to make that match would require A+1 edits.
Now look at B: this corresponds to the number of edits that were necessary to get the p-1 prefix of the pattern to match the text ending at position t. To get a match of the p prefix at the same position could be accomplished by either deleting that pth character from the pattern, or inserting the pth character into the text at that spot. (See the underlined red '1' in the table above.) So if this action were taken to obtain a match, we'd need B+1 edits.
Now look at C: this corresponds to the number of edits that were necessary to get the p prefix of the pattern to match the text ending at position t-1. To get a match of that same prefix at position t can be accomplished by deleting the new character from the text, or by inserting an additional character into the pattern. (See the underlined green '1' in the table above.) So if this action were taken to obtain a match, we'd need C+1 edits.
Now we can put the whole thing together. The value of "???" will be the minimum of the three possible values outlined above, corresponding to the three neighboring cells of the "???" cell. Here is the encoding of the algorithm.
Once the table is calculated, the bottomost row of the array corresponds to the edit distance required to match the entire pattern against all the substrings of the same length (9) in the text. The smallest value there is 3, at column 20. Thus the pattern can be converted to match the 9 character substring of the text ending at the 20th character of the text in 3 edits. That substring is EILAADEVL. That the edit distance between this substring and the 9-character pattern EIQADEVRL is 3 can be seen by placing the two strings atop each other like so:
EIQADEVRL -> EIQADEVL EILAADEVL -> EILADEVL
In the above text, I've used blue to indicate where a substitution could occur, and green to indicate where a deletion could occur. The strings on the right side of the diagram show what would result to pattern and text if the marked deletions were carried out.
It should be noted that using a deletion from one string to make it match the second is entirely equivalent to using an insertion in the second to make it match the first. The following diagram is similar to the first except now the right side shows what results when the green letters indicate where an insertion of that letter should take place in the opposite string.
EIQADEVRL -> EIQAADEVRL EILAADEVL -> EILAADEVRL
What do you think are the optimal run-time and space requirements for this algorithm?