Recursion -- Watching It Work
This is version 1.
This paper is intended for use by my undergraduate classes
where I can answer questions and explain notation and pseudo-code.
Use at your own risk.
Send corrections/comments to Susan Haynes' email: shaynes, on the host emich.edu
The first step to understanding recursion is to understand how it works.
The tool we'll use for observing recursion is, primarily, the activation tree.
The activation tree is grown in depth first order in a way that reflects the pushing
and popping of stack frames as a result of function calls and returns.
The activation tree can be used to follow along any collection of function
invocations, not just recursive ones.
To build an activation tree, start with the program code. The program code is
thought of as the executable, the activation tree can keep track of local variables,
parameters, return values and where you are in the execution. Usually, you only need to track
parameters, return value, and return address.
Constructing an activation tree is done by following these rules.
- In the code, if there is more than one recursive call, subscript each one
with {1, 2, ... }.
- When a function is invoked, draw a stack frame and make it the rightmost
child of the caller. The cursor is placed in the called node (i.e., it moves
from parent to child). The first function invoked is the root node.
- In the left box of the stack frame, place parameter values.
Label the stack frame with the callee's function name, including subscript.
- When you complete execution of the called function, put the return value
in the right box of the stack frame, then move the cursor up to the parent
(i.e., back to caller). You return to the location in the executable that corresponds
to the callee's name (i.e., you return to the point in the code where the subscript
matches the subscript of the returning (callee) function.
- Note, in returning from a callee that is a subscripted function, say
fun3(), you return to the point where the executable
called fun3(). If there is a return value, conceptually replace
fun3() with the return value.
- Note, parameter values must be computed before the function using those values can be
called. This includes parameters that are computed through a recursive call
(e.g., Ackermann's function).
Try this on a non-recursive set of functions.
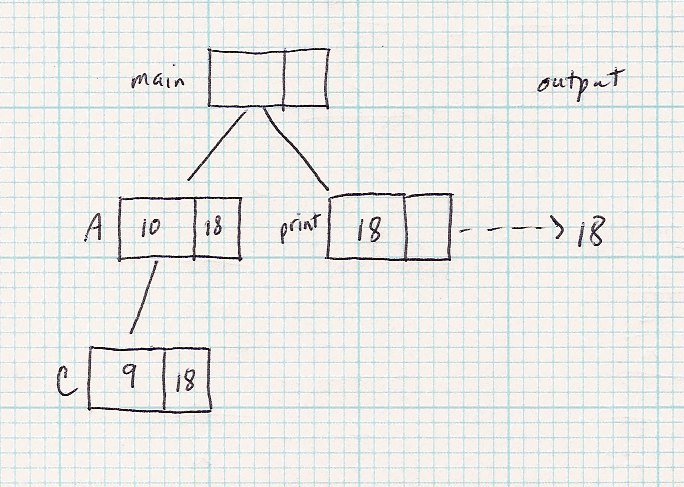
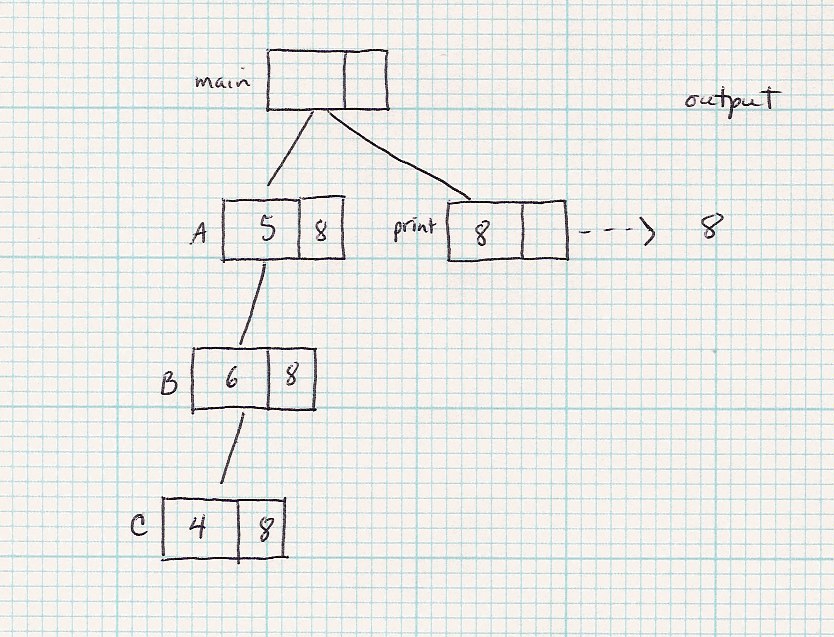
| Code | Suppose x = 10; | Suppose x = 5; |
int A(int m) {
if (m < 10) return B(m+1);
else return C(m-1);
}
int B (int m) {
if (m == 10) return 3;
else return C(m-2);
}
int C(int m) {
return m * 2;
}
void main () {
int x = ... ;
print ( A (x) );
}
|
|
|
| Q: When returning from A(10) with value 18, where am I?
Ans: In main. I've just calculated the parameter to print()
| Q: Where am I in the code after I return from B(6) with value 8?
Ans: In A(). I've just calculated the value that will be used in the
first return statement in A().
Q: Where am I after I return from C(4) with value 8?
Ans: In B(). I've just calculate the value that will be used in the
second return statement in B().
|
NOTE. I can stop tracking at any intermediate stage of execution, and from the activation tree be able to
quickly determine where I am in the code!
In thinking about the basic principles of recursion , get in your mind:
- What is the base case(s),
- For the recursive call(s):
- How do you reduce the set you're working on?,
- What is the construction you do with the result of the recursive call? (the answer may be "none")
- What do you do before or after the recursive call?
Example: Compute factorial, n!
0! = 1
n! = n * (n-1)!
The base case is n==0.
In re the recursive call:
The reduced set is n - 1
The construction is *
int fact(n) {
if (n==0) return 1;
else return n * fact (n - 1);
}
Now use the tree to track what happens when computing the Fibonacci number.
| Code | fib(3) |
int fib(n) {
if (n==0) return 1;
if (n==1) return 1;
return fib1(n-1) + fib2(n-2);
}
|
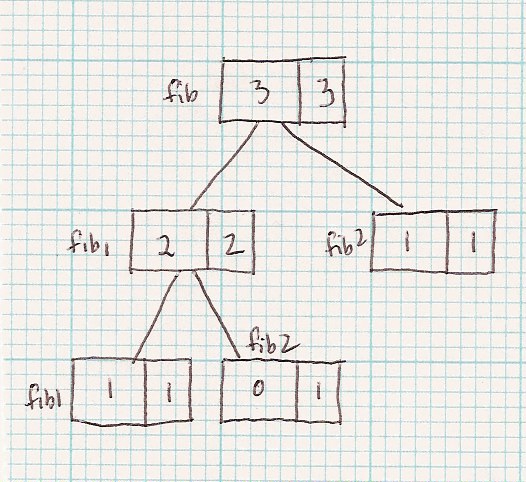 |
The base cases are n==0 and n==1.
The reduced sets are n-1 and n-2.
The construction is +.
Here's the tree for invoking fib(5)
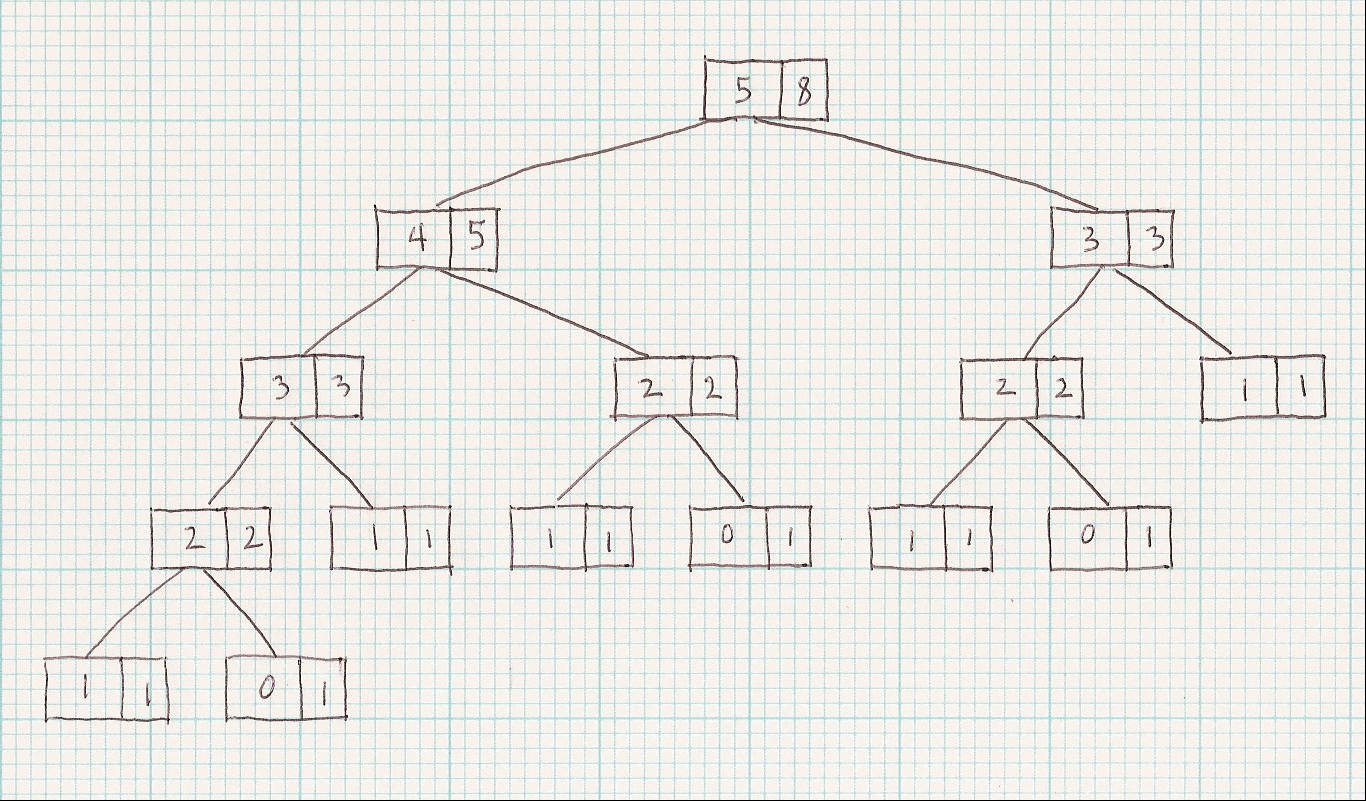 |
Note:
fib(3) appears 2 times
fib(2) appears 3 times
fib(1)appears 6 times!
Altogether, there are 15 invocations of fib for fib(5)
|
The next program will count the number of elements in a linked list.
| Here's a generic linked list |
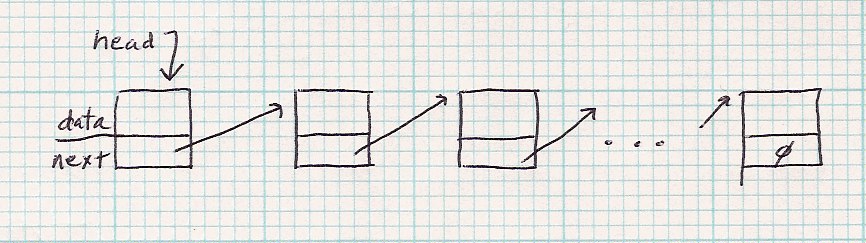 |
The base case is (head==null).
In re the recursive call:
The reduced set is head.next
The construction is increment by 1 (1+count() )
| Let's use this list, where the addresses are explicitly given. |
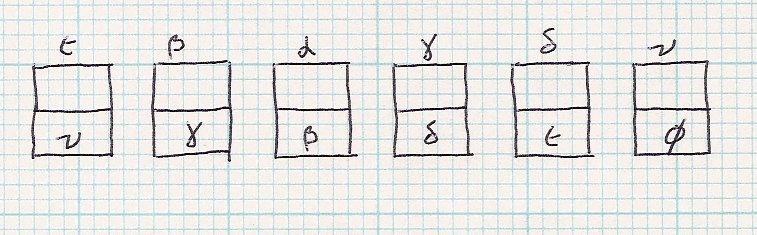 |
| Code | count(α) |
int count ( head ) {
if (head == null) return 0;
return 1 + count (head.next);
}
|
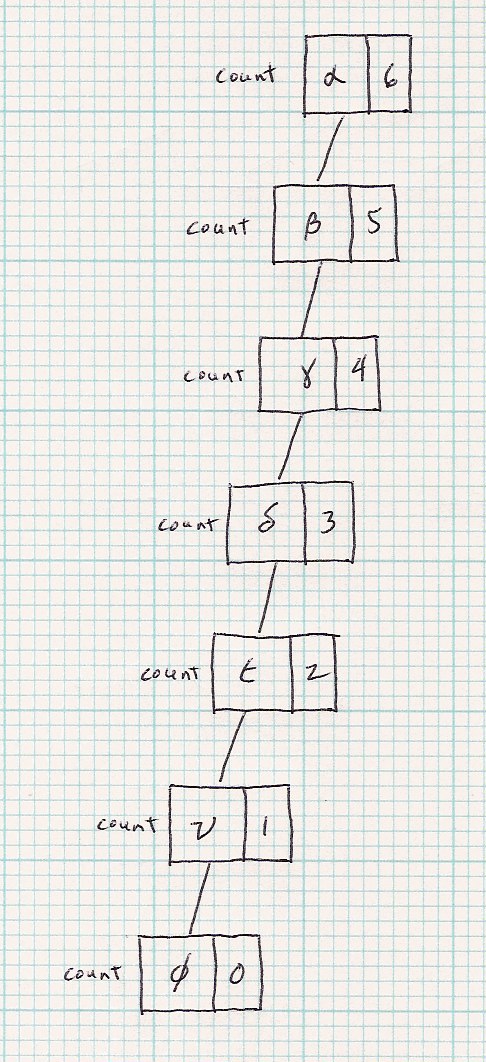 |
Check out how the stack frames form a linked list (that never actually exists
at one time in memory!) that is the same as the linked list structure!
Why is that?
Note the return values count up from 0 to 6, giving the length of the list
as specified by the current head of the list.
Trace the recursive program to print out the elements of a linked list.
| Let's use this list, where the addresses are explicitly given. |
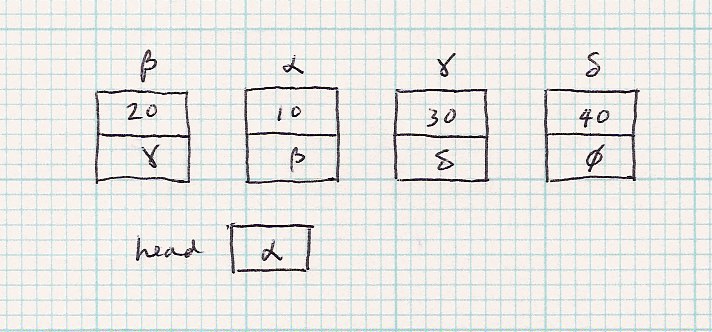 |
| Code | printList(α) |
void printList(α) {
if (head==null) return; // base case
else {
print (head.value); // do before call
printList(head.next); // note reduced set
return; // could have combined with previous
}
}
|
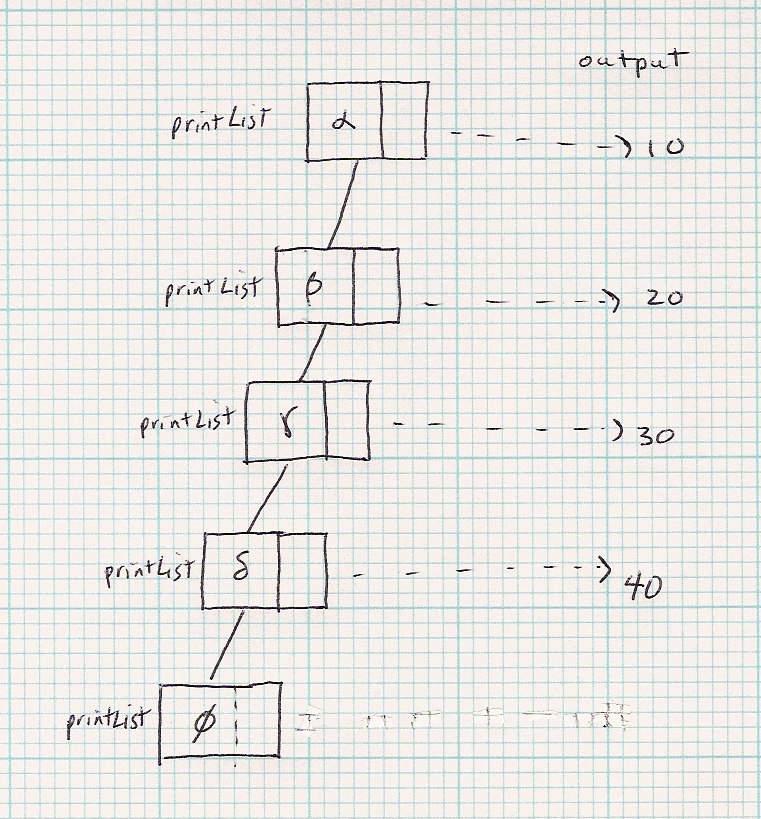 |
Trace this slightly modified recursive program to print a list in reverse
order using the same list.
| Code | printList(α) |
void printList(α) {
if (head==null) return; // base case
else {
printList(head.next); // note reduced set
print (head.value); // do after call
return; // could have combined with previous;
}
}
|
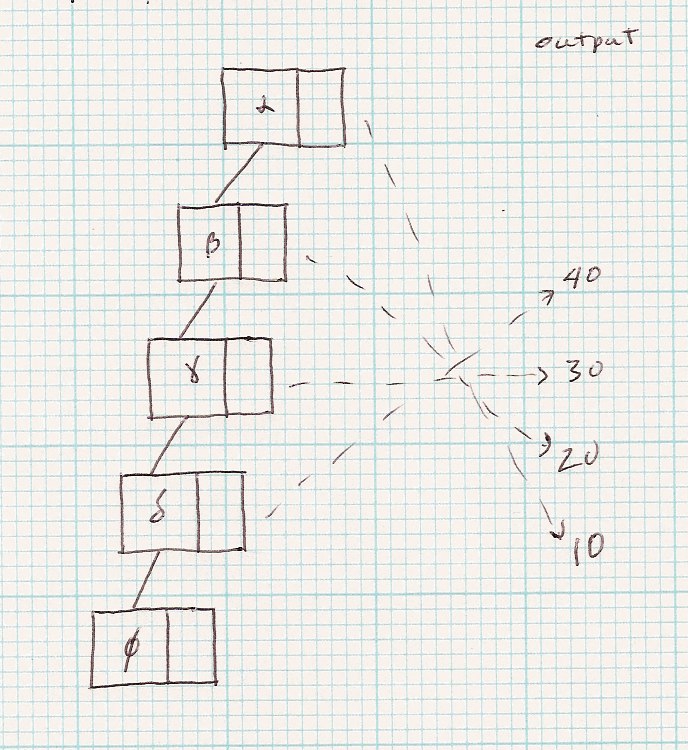 |
Use a recursive program to insert a new element at the end of a singly linked list.
What is the base case? p == null
For the recursive call, what is the reduced set? head.next
What is the construction? None, instead the "work" is done via assignment (=).
| Let's use this list, where the addresses are explicitly given. |
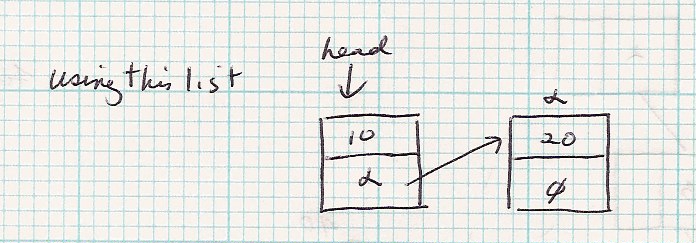 |
| Code | Node * insertAtEnd(Node * head, Node * n) |
void Node * insertAtEnd(Node * head, Node * n) {
if (head==null) return n; // base case
else {
head.next = insertAtEnd (head.next, n);
return head;
}
}
void main () {
Node * head = null;
. . .
Node * n = new Node (data, null);
. . .
head = insertAtEnd(head, n); // A
. . .
}
Note at the A comment, I need to make the head assignment,
because each head.next is being modified all the way back out
of the recursion.
|
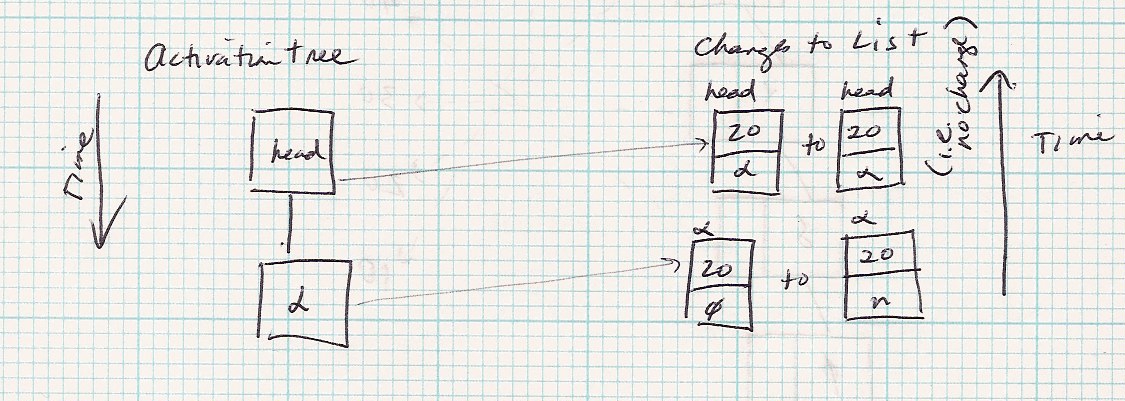 |
Do these:
- Trace towers of hanoi for n = 4.
- Write recursive code to sum the elements in an array --
the sentinel value is -1 (used to indicate the end of the array, don't use the array size)
- Write a recursive version of
// compute inner product, sentinel is -1
c = 0;
for (int i = 0; i < n; i++)
c += a[i] * b[i];
- Write recursive code to create a second list, which is the reverse order of a
first (singly linked) list.
- Write recursive code to insert an element at the end of a doubly linked list.
- Write recursive code to insert an element in sort order of a singly linked list.
This paper, even in this draft edition, must be properly cited if you make any use of it.
For a published, shorter version, see Haynes, SIGCSE 1995, Recursion for the Beginner (or something
like that).