Here's the problem: A woman standing on a hill sees a flagpole that she knows is 60 ft tall. The angle of depression to the bottom of the pole is 14\(^{\circ}\), and the angle of elevation to the top of the pole is 18\(^{\circ}\). Find here distance \(x\) from the pole.

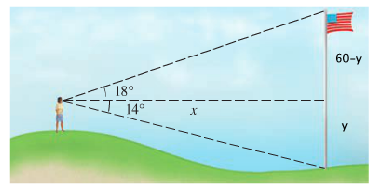
Here's the picture. Notice that I had to add \(y\) and \(60-y\) to parts of the flagpole whose lengths I don't know:

We see two different right triangles. Note that adding the two angles to get 32\(^{\circ}\) doesn't get us anywhere, as that 32\(^{\circ}\) is not part of any right triangle in the picture.

Using the top right triangle, we get the following equation: \[\tan(14^{\circ}) = \frac{y}{x}.\] Using the bottom right triangle, we get the following different equation: \[\tan(18^{\circ}) = \frac{60-y}{x}.\] We now have two equations in two variables, a kind of problem they prepare you well for in algebra! We're going to solve equation for \(y\), then set our two expressions for \(y\) equal to each other: \[y = x\tan(14^{\circ})\] and from the second equation we get \[y = 60-x\tan(18^{\circ}).\] Both of these \(y\)'s stand for the same distance in the picture, so we know they're equal to each other: \[x\tan(14^{\circ}) = 60 - x\tan(18^{\circ})\] Getting all the \(x\)'s on one side gives us \[x\tan(14^{\circ}) + x\tan(18^{\circ}) = 60\] Now pull the \(x\) out on the left side to get \[x(\tan(14^{\circ})+\tan(18^{\circ})) = 60\] then divide by all the stuff next to \(x\) to finish the problem: \[x = \frac{60}{\tan(14^{\circ}) + \tan(18^{\circ})} \approx 104.485 \; \mathrm{ft},\] correct to three decimal places.