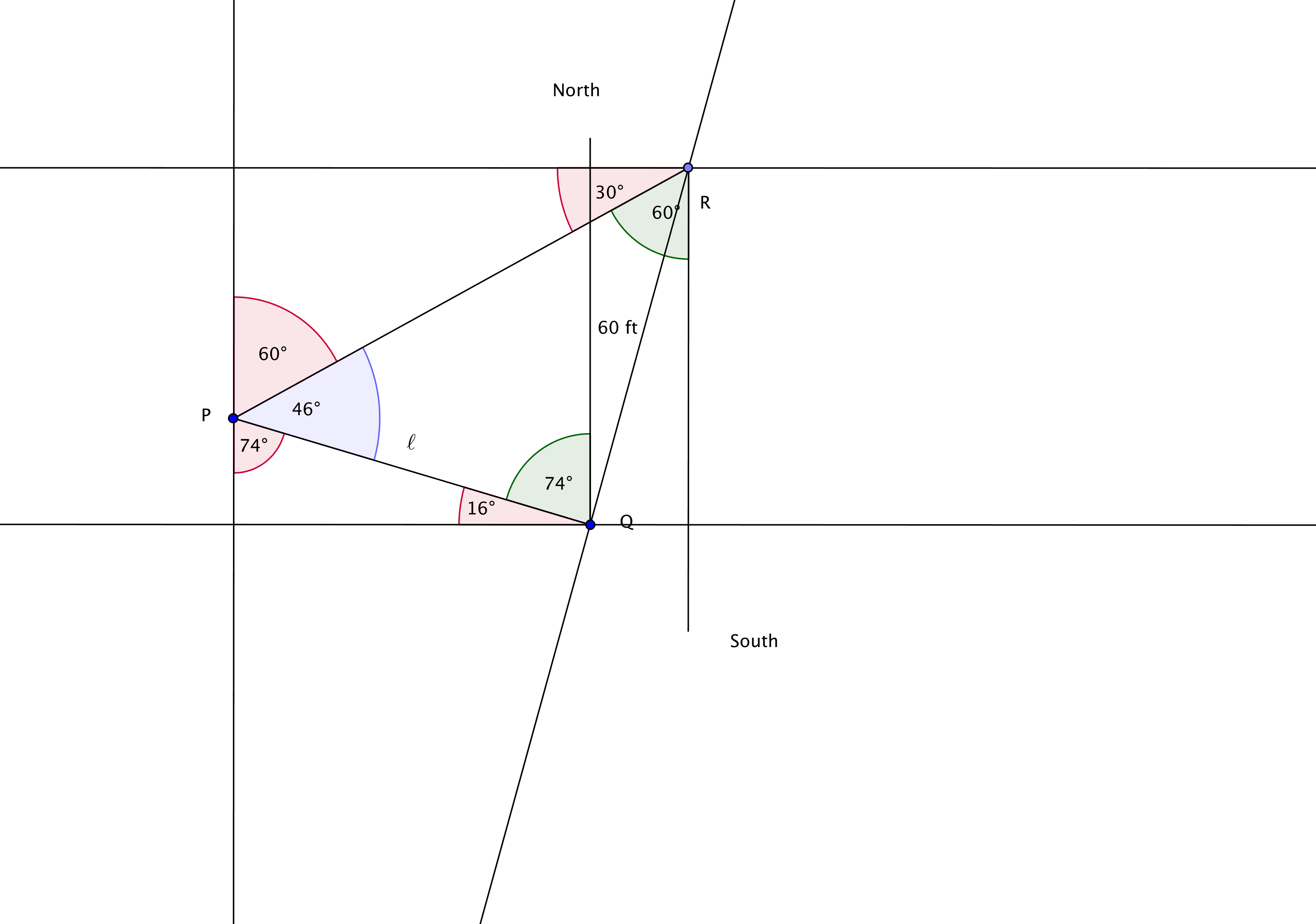
A Bearing Problem With Solution
We now have a right triangle and enough information to finish the problem! Note that for
our \(56^{\circ}\) angle, the opposite side has length 60, and the adjacent side has
length \(\ell\). So, using tangent, we get
\(\displaystyle{\tan(46^{\circ}) = \frac{60}{\ell}},\)
so that
\(\displaystyle{\ell = \frac{60}{\tan(46^{\circ})} \approx 57.9413264\underline{9}}.\) ft.