I always want to hear your thoughts on the class so far, so I created an online form for anonymous feedback. Please use it to let me know what you think (or if you are not concerned about anonymity, just send an email) :
https://docs.gooREMOVETHISgle.com/spreadsheet/embeddedform?formkey=dDF2U2djSDAtRmFUM0NsTllmOFJ2ZFE6MQ
You can use this throughout the semester. You should remove the REMOVETHIS; I just put it in there to deter automated webcrawlers.

Ethics

The American Statistical Association (ASA) has a statement of Ethical Guidelines for Statistical Practice

The Institute for Operations Research and Management Science (INFORMS) has a Certified Analytics Professional program that includes this Code of Ethics.

And here is a slightly more light-hearted code, originally written for a financial setting:

Emanuel Derman’s Hippocratic Oath of Modeling

• I will remember that I didn’t make the world and that it doesn’t satisfy my equations.
• Though I will use models boldly to estimate value, I will not be overly impressed by mathematics.
• I will never sacrifice reality for elegance without explaining why I have done so. Nor will I give the people who use my model false
comfort about its accuracy. Instead, I will make explicit its assumptions and oversights.
• I understand that my work may have enormous effects on society and the economy, many of them beyond my comprehension.

Some papers to consider:
Ethical Statistics and Statistical Ethics: Making an Interdisciplinary Module
Critical Values and Transforming Data: Teaching Statistics with Social Justice

And a report on how web sites return different search results, prices, or ads based on the apparent race or location of the searcher:http://www.wnyc.org/story/dba2f97dd61e2035fd433a48/?utm_source=/story/128722-prime-number/&utm_medium=treatment&utm_campaign=morelikethis

searching for a traditionally black-sounding name such as “Trevon Jones” is 25 percent more likely to generate ads suggesting an arrest record—such as “Trevon Jones Arrested?”—than a search for a traditionally white-sounding name like “Kristen Sparrow,” according to a January 2013 study by Harvard professor Latanya Sweeney. Sweeney found this advertising disparity even for names in which people with the white-sounding name did have a criminal record and people with the black-sounding name did not have a criminal record.

And later in the report,

Our tests of the Staples website showed that areas with higher average income were more likely to receive discounted prices than lower-income areas.

The Big Picture (Bigger than Statistics)

Statistics is its own field, of course, but it is related to many others. People now talk about Analytics, which is often broken into

· Descriptive Analytics: what did happen? (EMU Math 360)

· Predictive Analytics: what will happen? (EMU Math 360, EMU Math 419W)

· Prescriptive Analytics: what’s the optimal thing to do? (EMU Math 319, EMU Math 560)

Some people summarize this as Describe, Anticipate, Decide = D.A.D.

Of course other EMU statistics courses relate to Descriptive and Predictive analytics; I’ve only listed the ones I teach.

“Data Science” is another hot term these days. Some say it’s a combination of Statistics/Math/Operations Research, Computer Science, and Substantive Expertise:

http://drewconway.com/zia/2013/3/26/the-data-science-venn-diagram

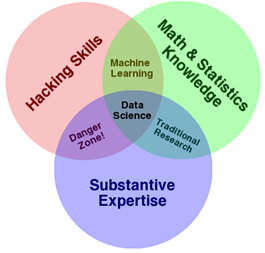
The book “Doing Data Science”, page 42, says "Now the key here that makes data science special and distinct from statistics is that this data product then gets incorporated back into the real world, and users interact with that product, and that generates more data, which creates a feedback loop."

I disagree with that on two levels: first, plenty of people do what they’d call data science that doesn’t interact with users/create a feedback loop, and second, the idea of interaction or creating a feedback loop could still be called statistics, or Advanced Analytics/prescriptive analytics.

“Big Data” is also a hot topic these days. You could say it is any data set that is too big to fit onto one computer, and must be split across multiple computers. For example, Facebook profiles and clickstreams would constitute big data; some physics experiments also generate big data (100 TB per day!) Big data is often characterized by the “3 V’s”: Volume, Velocity, and Variety. Volume means how much data there is, Velocity means how fast it comes in, and Variety is the mix of numbers, text, sounds, and images. We won’t be dealing with Big Data in this class, but ask me if you want to know more about it.

The Big Picture (just inside this class)

We will use Excel a lot, even though there are well-documented problems with it for statistics; for example,

http://panko.shidler.hawaii.edu/SSR/Mypapers/whatknow.htm

http://www.analyticbridge.com/profiles/blogs/comprehensive-list-of-excel-errors-inaccuracies-and-use-of-wrong-

Concept maps of Statistics

http://derekbruff.org/blogs/math216/?p=675

http://bioquest.org/numberscount/statistics-concept-map/

http://iase-web.org/documents/papers/icots6/5a2_bulm.pdf

http://cmapskm.ihmc.us/rid=1052458963987_1845442706_8642/Descriptive%20statistics.cmap
http://cmapskm.ihmc.us/servlet/SBReadResourceServlet?rid=1052458963987_97837233_8644&partName=htmltext

http://www.sagepub.com/bjohnsonstudy/maps/index.htm

Eight Big Ideas

1. Data beat anecdotes
2. Association is not causation
3. The importance of study design
4. The omnipresence of variation
5. Conclusions are uncertain.
6. Observation versus experiment
7. Beware the lurking variable [confounding]
8. Is this the right question?

http://www.statlit.org/pdf/2013-Schield-ASA-1up.pdf

What Your Future Doctor Should Know About Statistics: Must-Include Topics for Introductory Undergraduate Biostatistics
Brigitte Baldi & Jessica Utts
Pages: 231-240
DOI: 10.1080/00031305.2015.1048903

What do Future Senators, Scientists, Social Workers, and Sales Clerks Need to Learn from Your Statistics Class? http://www.ics.uci.edu/~jutts/APTalk.pdf

1. Observational studies, confounding, causation 2. The problem of multiple testing 3. Sample size and statistical significance 4. Why many studies fail to replicate 5. Does decreasing risk actually increase risk? 6. Personalized risk 7. Poor intuition about probability/expected value 8. The prevalence of coincidences 9. Surveys and polls – good and not so good 10. Average versus normal

Math Is Music; Statistics Is Literature

Richard D. De Veaux, Williams College, and Paul F. Velleman, Cornell University

S even unnatural acts of statistical thinking:
➊ Think critically. Challenge the data’s credentials; look for biases and lurking variables.
➋ Be skeptical. Question authority and the current theory. (Well, okay, sophomores do find this natural.)
➌ Think about variation, rather than about center.
➍ Focus on what we don’t know. For example, a confidence interval exhibits how much we don’t know about the parameter.
➎ Perfect the process. Our best conclusion is often a refined question, but that means a student can’t memorize the ‘answer.’
➏ Think about conditional probabilities and rare events. Humans just don’t do this well. Ask any gambler. But, without this, the student can’t understand a p-value

7 Embrace vague concepts. Symmetry, center, outlier, linear … the list of concepts fundamental to statistics but left without firm definitions is quite long. What diligent student wanting to learn the ‘right answer’ wouldn’t be dismayed?

Statistics Habits of Mind http://info.mooc-ed.org.s3.amazonaws.com/tsdi1/Unit%202/Essentials/Habitsofmind.pdf

● Always consider the context of data ● Ensure the best measure of an attribute of interest ● Anticipate, look for, and describe variation ● Attend to sampling issues ● Embrace uncertainty, but build confidence in interpretations ● Use several visual and numerical representations to make sense of data ● Be a skeptic throughout an investigation

Proposal/Project Guidance

For project proposals, a few things to remember:
* I encourage team projects, but solo projects are allowed as well.

* Team sizes are limited to 2 people (arranged with whomever you want).

* if anyone is looking for a partner, please let me know and I will do my best to play eHarmony.

* There is no competition for project topics. Multiple people or teams may do the same project.
* I STRONGLY ENCOURAGE you to chat with me about project ideas well before the proposal deadline, either in person or by email.
* After the chatting is done, feel free to email me a draft of a proposal (and perhaps a data set) for some informal feedback.
* See below some sample project titles from last year's Math 360 class.
Proposals
Proposals will generally be 1 to 2 pages, and will contain:
* title of project
* author(s) names
* a description of the problem you are facing
* a description of the available data or data collection plans (incl. a copy of the data if it’s already available, perhaps as a separate file)
* a description of the proposed analysis
* literature search? for many projects, no literature search is needed. Others may benefit from a literature search, and may get bonus points for doing one. Giving proper credit to your sources of information or ideas is always required.
* data? If you already have the data, include a spreadsheet of it as a 2nd file when you upload the presentation

If your project idea depends on getting a data set from your boss at work, you need to have the data set in hand by the time of the proposal. I've had a few projects go bad when a boss doesn't come through with promised data.

A proposal does not lock you in to a topic or analysis method. If your project is not working out, contact me immediately and together we will find a new project topic.

Procedural Advice: CI vs HT, and Controls

A general tip as you're doing your projects: doing confidence intervals is almost always better than doing a hypothesis test, because a CI can be converted into an HT very easily in your head (did the CI include zero? for example), but knowing the results of an HT doesn't give you much info about the related CI. There are some projects where a CI isn't applicable, though--often those related to Chapter 12 (chi-squared tests). The one nice thing about HT, though, is that you get a P-value, while the CI just lets you know that it was < 0.05 or whatever value you used for a CI.

It's important to create artificial data sets similar to what your real data set is. That way, when you do your processing, you can tell if you are getting what you expect to get--it's a way of debugging. You start by copying the file with your original data set, then in that copy, replacing the original data with artificial data. Then you do your analysis on the artificial data. Once you've done it for artificial data, you should be able to save another copy of that file, then paste your real data in where the artificial data is, and have all the calculations automatically update. This is vastly better than trying to re-create the formulas in a new sheet, since that could introduce new bugs.
To generate a Standard Normal in excel, use
=norminv(rand(),0,1)
To generate a non-standard normal with mean 5 and std.dev. 3, use
=norminv(rand(),0,1)*3 + 5
Another big advantage of creating artificial data is then you can compute how much your output measurements change just due to random chance, by running a whole bunch of random trials.

Someone asked me if the random number generator in Excel is seedable (that is, can it be set to start at the same sequence over and over). There's no interface for doing that, but I researched the algorithm that the random number generator uses, and I've implemented it in simple formulas in a posted spreadsheet. You may ignore this if you want.

Another key component of some projects is the idea of Cross-Validation. Instead of fitting models to the entire data set, you pick a portion of it called the “Training” set and fit the models to that. Then you use those fitted models to make predictions for the rest of the data, called the “Test” set, to see which model does the best. Actually, if you then want to quantify the prediction errors you might expect to see, you need a 3^rd portion of the data set: you fit the winning model to the training & test set, then make predictions for that 3^rd portion, and measure the prediction error.

Doing Data Science says:

In-Sample, Out-of-Sample, and Causality
We need to establish a strict concept of in-sample and out-of-sample data. Note the out-of-sample data is not meant as testing data—that all happens inside in-sample data. Rather, out-of-sample data is meant to be the data you use after finalizing your model so that you have some idea how the model will perform in production. We should even restrict the number of times one does out-of-sample analysis on a given dataset because, like it or not, we learn stuff about that data every time, and we will subconsciously overfit to it even in different contexts, with different models.
Next, we need to be careful to always perform causal modeling (note this differs from what statisticians mean by causality). Namely, never use information in the future to predict something now. Or, put differently, we only use information from the past up and to the present
moment to predict the future. This is incredibly important in financial modeling. Note it’s not enough to use data about the present if it isn’t actually available and accessible at the present moment. So this means we have to be very careful with timestamps of availability as well as timestamps of reference. This is huge when we’re talking about lagged government data.

Final Report

Your final report should be a roughly 5-to-10-page technical report (a Word file, usually). I don’t count pages, though, so don’t worry about the exact length. Please use the HomeHealthCare.doc file that I will email out as a template (remove their content, type in your own content).

Please upload both your report file and your Excel file at the same time. But, your report should have copies of any relevant figures; don't just say "see the Excel file".

If you are part of a team project, _each_ person should upload a copy of the presentation and report.

Presentations

For your final presentation, you have 2 options:

· A 5-minute Powerpoint-style presentation that you stand up and give to the class (roughly 5 slides), or

· A poster presentation, which often consists of about 12 Powerpoint slides, printed out on paper and taped to the wall of the classroom (don’t buy/use posterboard).

Each person or team of 2 may decide whether they want to do a poster or oral presentation. Either way, presentation materials should be uploaded to a dropbox inside EMU-online.

Please do not feel obligated to dress up for our presentation day in Math 360. Anyone who does dress up will be a few standard deviations from the mean, as statisticians say. Either way, it will not affect your grade at all.

However, it is important to present in a professional way (aside from how you are dressed). If I write a letter of recommendation for you, I want to be able to say how polished your presentation was—not just your slides, but your manner of speaking. This can be especially important for future teachers. In a letter of recommendation I would hope I could say “While I’ve never observed ____ as they teach an actual class, their final project presentation in Math 360 convinces me that they have the presentation skills to be a great teacher.”

National Competition
I will recommend that some people submit their work to the Undergraduate CLASS Project Competition (USCLAP)
http://homepages.dordt.edu/ntintle/usproc/USCLAP.htm
The writeup for that has the following page limits (all in 11-point Arial, single-spaced, 1-inch margins):

1 page for title and abstract

<=3 pages for report

1 page for bibliography, if any (optional)

<=5 pages for appendices

So you might want to format your paper that way if you’re thinking of entering the contest.

Note that if you are using data from human subjects (or animals!) you will need to apply for permission from EMU’s Institutional Review Board (IRB) to use your data in the USCLAP contest. I can help you with this, but we need to do it early in the semester. If you aren’t hoping to submit to the USCLAP, then IRB approval is usually not required.

The judging criteria for that contest will be the basis of the grading system for projects:
1. Description of the data source (15%)
2. Appropriateness and correctness of data analysis (40%)
3. Appropriateness and correctness of conclusions and discussion (20%)
4. Overall clarity and presentation (15%)
5. Originality and interestingness of the study (10%)
NOTE: All essential materials addressing these criteria must be in the report, not confined to the spreadsheet file.

You can see the guidelines I give to my other project-based classes (Math 319, Math 419, Math 560) at this link:
http://people.emich.edu/aross15/project-guides/guides.html
though as you can see from the above, the requirements for Math 360 are a little different because of the statistical focus.

Also see:

Heiberger, Richard M., Naomi B. Robbins, and Jüergen Symanzik. 2014. "Statistical Graphics Recommendations for the ASA/NCTM Annual Poster Competition and Project Competition", Proc. of the Joint Statistical Meetings, American Statistical Association, Arlington, VA.

Symanzik, Jüergen; Naomi B. Robbins, Richard M. Heiberger. (2014). "Observations from the Winners of the 2013 Statistics Poster Competition --- Praise and Future Improvements." The Statistics Teacher Network, 83, 2-5.

Sample project titles from previous years

Baseball player builds and home runs
Tennis serve accuracy
Noll-Scully simulation of sports rankings
Spring Training vs Regular Season
Anchoring effect
Finding a Piecewise Linear Breakpoint in Chemistry data
Music participation and GPA
double-SIDS dependencies
Swimming times
Salary vs. Results in NCAA Tournament
NBA scores
Barbie Bungee Challenge
Incumbency advantage in elections
Comparing Distinct Audio Points in Classical and Rock Music
Barbie Bungee Challenge
Airbags, seat belts, bike helmets
Spring Training vs Regular Season
Golden Ratio in Art
Gender differences in SAT scores

Home health care data
double-SIDS dependencies
GEAR-UP survey data
Normal distributions on Wall Street?
NBA scores
Naive Bayesian spam filtering
Honors college GPAs
Predicting Course Grades from Mid-Semester Grades
Anchoring effect
Salary vs. Results in NCAA Tournament
Incumbency advantage in elections

An Analysis of Correlations between Event Scores in Gymnastics Using Linear Regression

Accounting Fraud and Benford's Law

Appointment-Based Queueing and Kingman's Approximation

Are Consumers Getting all the Coconut Chocolaty Goodness They’re Paying For?

Are regular M&Ms more variable in weight than Peanut M&Ms?

Barbie Bungee Experiment

Breaking Eggs in Minecraft

Calculus-Based Probability

Comparing the Efficiency of Introductory Sorting Algorithms

Distribution of File Sizes

Do students who score better on a test’s story problems score better on the test as a whole?

Do studying Habits affect your interest in math

Do young adults under 18 and 18 and older have the same completion rate of the 3-shot regimen for Gardasil?

Does age effect half-marathon completion time

Patterns in bulk discounts

Does having high payrolls mean you will win more Major League Baseball games?

Gardasil 3-shot vaccine completion, average number of shots

Getting Hot at the Right Time: A statistical analysis of variable relative strength in the NHL

Home Field Advantage in MLB, NFL, and NBA

How random are Michigan Club Keno and Java random numbers?

Ice Cream Sales and Temperature

Is there relationship between the length of songs at the #1 spot on the Billboard Hot 100 and their respective week at #1 in time?

Lunch vs Dinner Sales at Domino's

Math Lab demand data vs Section Enrollment by Hour

Modeling School of Choice Data in Lenawee County

Pharmacy prescription pick-up times

Piecewise-Linear Regression on Concentration / Conductivity Data

Proportion & Probability of 2-Neighborly Polytopes with m-Vertices in d-Dimensions

Ranking Types of Math Questions (Algebra-based)

Scoring Trends and Home Court Advantage in Men’s College Basketball

Skip Zone on the Sidewalk

Spaghetti Bridge and Pennies

What affects a pendulum’s behavior

Project Ideas

While these are shown in various categories, each project idea is open to anyone in any major.

Miscellaneous

Are stock prices (or percent returns) normally distributed? See http://bestcase.wordpress.com/2010/08/01/outliers-in-the-nyt-reflections-on-normality/

Various questions on where the Daily Double in Jeopardy is located (ask me for more thoughts)

Song database: http://musicbrainz.org/doc/MusicBrainz_Database

correlation between LSAT, GPA, admission, and salary; ask me to dig the data out of my email if needed

Fermat's last theorem histogram: how close can the equation come to being true?

* Mega M&Ms claim they have "3x the chocolate per piece"
* What is the speed of the wave as dominoes tumble in a row, as a function of the spacing between them? Is it a linear function?
* If people close their eyes and balance on one foot, how long can they stay up? Does it depend on which foot they stand on, vs. their handedness?
* If you do some moderate exercise then track your pulse after you stop, does it go back to your resting pulse in a linear fashion? exponential? power?
* psychology/occupational therapy: learning curves,
http://web5.uottawa.ca/www5/dcousineau/home/Research/Talks/2001-06_BBCS/2001-06_BBCS-learning.pdf
* Does the "close door" button on elevators actually do anything?
* which packs more efficiently, plain M&Ms or spheres?
* burning birthday candles,
http://www.algebralab.org/activities/activity.aspx?file=Science_BurningCandles.xml
http://www2.drury.edu/fred/activities/candles/candle.html
* can you do anything with the loud hand driers in the Pray-Harrold bathrooms?
* as you add layers of tape (or post-it notes?) over the camera of an iPhone/iPad/Android, how does the total light transmitted to the camera vary?
* How long a toaster takes vs. the control setting (or, how dark the toast gets?)

* how fast does water flow out of an I.V. (intravenous fluid) bag, based on how high the bag is to where the outflow is?

Economics

https://en.wikipedia.org/wiki/Cliometrics

Cliometrics is the study of history and economics using mathematical methods.

* business cycle durations and/or models; see http://onlinelibrary.wiley.com/doi/10.3982/ECTA8050/abstract?elq_mid=4373&elq_cid=1272383

* How much seasonal effect is there in things like inflation, stock prices, stock indices, etc.?
- try this: separate data into months, do ANOVA to see if there's a difference between months (or use quarters)
- should you operate on the actual value, or the % change, or Ln( new/old ) ?
- or try triple-exponential smoothing (also called Holt-Winters) and see what seasonal effects it finds
- also use artificial data that has no seasonality, and artificial data that definitely does have seasonality

* How much correlation is there from day to day (or week to week, or month to month, or year to year, or hour to hour, or minute to minute, etc.) in inflation, stock prices, stock indices, etc?
- should you operate on the actual value, or the % change, or Ln( new/old ) ?

* Do stock prices, etc. have a Normal distribution?
- should you operate on the actual value, or the % change, or Ln( new/old ) ?
- if the data is correlated from day to day, consider taking data from separate days rather than adjacent days.
- use the correlation coefficient on a Q-Q normal probability plot as a way to do a hypothesis test (see that part of the textbook for details--chapter 7)

* explore Hyperbolic Discounting: the way actual people might (or might not) treat the value of money in future time periods. Do a survey and ask how much money people would trade now for a specified payoff in the future, then fit a function to it. Also, there is a hypothesis that one's native language can have an effect (or is at least correlated with) on how one views the value of future money, so consider separating results by the person's native language.

Various data is at
http://www.econlib.org/library/sourcesUS.html

Physics

toy helicopter lift force vs rotation speed http://sphsdevilphysics.weebly.com/uploads/5/0/7/1/5071691/example02_en.pdf

GPS accuracy:
- by time of day
- by weather/day-to-day
- within span of a few seconds or minutes
- from device to device

Tablet/Smartphone Accelerometer Data:
- accuracy at 500 Hz vs 50 Hz vs 5 Hz
- correlation between devices

Mars Craters data set, craters.sjrdesign.net

Make your own crater data set with a bucket of sand and a heavy marble?

cepheid variable stars; ask me to dig data out of my email box

Asteroid size distribution: can get data from http://www.asterank.com http://www.minorplanetcenter.net/iau/lists/Dangerous.html
http://earn.dlr.de/nea/table1_new.html
http://earn.dlr.de/nea/

http://www.space.com/30197-saturn-rings-math-rule.html?cmpid=514630_20150815_50643176&adbid=10153004255456466&adbpl=fb&adbpr=17610706465 and http://www.pnas.org/content/112/31/9536
Size distribution of particles in Saturn’s rings from aggregation and fragmentation
Nikolai Brilliantov , P. L. Krapivsky , Anna Bodrova, Frank Spahn, Hisao Hayakawa, Vladimir Stadnichuk, and Jürgen Schmidt

space weather, Coronal Mass Ejections CME (ask me to dig up some data on this out of my emails)

There’s a new ASA section on astrostatistics, described in AMstat News—see what they do?

http://en.wikipedia.org/wiki/Proton_decay In an experiment involving a series of particle collisions, the amount of generated matter was approximately 1% larger than the amount of generated antimatter. The reason for this discrepancy is yet unknown.[2]

V.M. Abazov et al. (2010). "Evidence for an anomalous like-sign dimuon charge asymmetry". arXiv:1005.2757. http://arxiv.org/abs/1005.2757

Future Teachers

Tennessee STAR study on small class sizes

problems with estimating from pie charts

parents probability of pulling kids from public schools (survey)

Regression through the origin: when?

Instead of a regular project, work on getting the Data Analysis electronic badge?

anchoring effect

Barbie Bungee: make a bungee-cord out of rubber bands, and send a Barbie (or similar toy) plunging toward the floor. Try it with a few different lengths of cord, record how far she plunges, then forecast how many rubber bands would be needed for a 12-foot drop. You can find more info online, of course.

Spaghetti Bridges: make a simple bridge of straight spaghetti (not glued into a truss), see how much weight it can hold. Repeat with wider spans and/or more strands per bridge. You can find more info online. One reference is “Slope-Intercept Form—Beam Strength” from Exploring Algebra 1 with TI-Nspire, 2009, Key Curriculum Press.

Pullback Cars

* How far does a supersoaker shoot, based on how many pumps you give it?
* How far does a supersoaker shoot, as a function of time as you hold down the trigger?

Statistics Majors

Here are some ideas about the mechanics of statistics:

LiveRegression formulas

Confidence interval on s_e for linear regression

Partial Correlation in multivariate analysis

Simulate a thought experiment on publication bias

advanced work on causality: http://magazine.amstat.org/blog/2013/08/01/causality-in-stat-edu/
Judea Pearl work on causality
Bayesian networks
Granger causality

Computer Science
Consider reading “Statistical Modeling: The Two Cultures”, which talks about the divide between traditional statistical methods and “machine learning” methods:

https://projecteuclid.org/download/pdf_1/euclid.ss/1009213726

Machine Learning problems: logistic regression, SVM, etc.

Cross-Validation: training and test data sets

Queueing simulation in Python (using existing code from Prof. Ross)chi

distribution of file sizes
- on a hard drive (correlated to time of creation, modification, or access?)
- on a web server
- as requested from a web server

distribution of packet sizes, and correlation from one to the next?

distribution of time gap between packets, and correlation from one to the next?

spam filtering; try the Enron email database at http://www.cs.cmu.ed/~enron

durations of jobs on the CPU

memory sizes of jobs

paging policies

Network round-trip times for pings

Sleep vs Cron repetitive wakings

look into what gets presented at ACM SIGMETRICS
http://sciencehackday.pbworks.com/w/page/24500475/Datasets
http://aws.amazon.com/datasets?_encoding=UTF8&jiveRedirect=1
http://www.cs.cmu.edu/~awm/15781/project/data.html

Health care
Medicare Home Health Compare

Gardasil data set:
http://www.amstat.org/publications/jse/v19n1/gardasil.txt

SEER cancer data set,
http://seer.cancer.gov/
(need to submit application to use it)

National Longitudinal Study of Adolescent Health, via IPCSR/umich (easiest to use wave 1)

Health Evaluation and Linkage to Primary Care (HELP), data set HELPrct from Project Mosaic

painkiller prescription and overdose rates by state; I have some of the data saved in an email

Sports

Pick your favorite sport and ask a statistical question about it. Some examples:
* predicting player performance from previous years (helpful first step to choosing a fantasy team)
* quantifying home-field advantage
* (harder) quantifying time-zone advantage
* bracketology

How consistent is a participant's performance (#fish? weight? rank? z-score?) from one event in the tour to the next? Compare to other individual-performance sports? Here are links for 3 tournaments in 2014:

http://www.flwoutdoors.com/bassfishing/flw/tournament/2014/7128/kentucky-lake-paris-landing-professional-results/?dpl=1&all=1&sr=1&rpp=50&&sort=pl

http://www.flwoutdoors.com/bassfishing/afs/tournament/2014/7134/potomac-river-professional-results/?dpl=1&all=1&sr=1&rpp=50&&sort=pl

http://www.flwoutdoors.com/bassfishing/afs/tournament/2014/7135/lake-champlain-professional-results/?dpl=1&all=1&sr=1&rpp=50&&sort=pl

How about the Hot Hand?

http://regressing.deadspin.com/the-myth-of-the-myth-of-the-hot-hand-1588112937

http://www.nytimes.com/2014/06/26/science/the-science-of-hot-hand.html?referrer=&_r=2

http://andrewgelman.com/2014/03/11/myth-myth-myth-hot-hand/

Here is a stats textbook that has a sports focus, rather than just doing sports-statistics, but it might still be interesting: http://www.sportsci.org/resource/stats/index.html

Related books and Websites

Statistical Applets:http://sapphire.indstate.edu/~stat-attic/index.php?topic_id=HT

GeoGebra can do some statistics: http://web.geogebra.org/beta/

use the three-bar button in the upper right
choose Perspectives
choose Spreadsheet&Graphics
click on the normal curve with an area under it
Play with either the Distribution or the Statistics tab
Statistics can do Z Test of a Mean, T Test difference of means, etc.

“Resampling: The New Statistics” by Julian L. Simon Second Edition published October 1997, free on the web

Excel 2010 for educational and psychological statistics : a guide to solving practical problems / Thomas Quirk.

Excel 2010 for biological and life sciences statistics : a guide to solving practical problems / by Thomas J. Quirk, Meghan Quirk, Howard Horton.

Converting Data into Evidence
A Statistics Primer for the Medical Practitioner
DeMaris, Alfred, Selman, Steven H.

Statistics with Excel website: http://www.real-statistics.com/

Little Handbook of Statistical Practice
http://www.jerrydallal.com/LHSP/LHSP.HTM

http://www.stat.berkeley.edu/~aldous/Real-World/draft_book.pdf
On Chance and Unpredictability: 13/20 lectures on the links between mathematical probability and the real world. David Aldous, January 2012

Statistical Reasoning in Sports, by Tabor and Franklin http://bcs.whfreeman.com/sris/

http://content.bfwpub.com/webroot_pubcontent/Content/BCS_5/SRIS/Student/Appendices/AppB_Using_Excel.pdf

Statistics: A Guide to the Unknown

Forty Studies that Changed Psychology: Exploration into the History of Psychological Research

"Making Sense of Data" volumes 1,2,3, by Glenn J. Myatt; EMU library has an electronic subscription

Doing Data Science: Straight Talk from the Frontline, By Cathy O'Neil, Rachel Schutt; Publisher: O'Reilly Media

Chapter 1

We will use this link for the Car Insurance activity:
https://docs.gooREMOVETHISgle.com/spreadsheet/embeddedform?formkey=dEV4M2hZanFqRlByRVRadWJiZTFQd3c6MQ

and then later we will use this link for the Data Types activity:
https://docs.gooREMOVETHISgle.com/spreadsheet/embeddedform?formkey=dERFS3VncWZHbUZMNnVVcnJwcXltYlE6MA
Some additional reading is included below.

To prepare for our next class, we will use the following PDF file on Random Rectangles:
http://www.rtmsd.org/cms/lib/PA01000204/Centricity/Domain/197/RandomRectangles.PDF
and you should enter your answers here before class starts:
https://docs.gooREMOVETHISgle.com/spreadsheet/embeddedform?formkey=dHN0SlctaDFNaTY2QWctS3RraHJZbWc6MQ

Data Types

Sometimes we code binary categorical variables (like gender) as 0 or 1; that’s called Dummy coding. We can also code them as -1 vs +1; that’s called Effect coding: http://methodology.psu.edu/node/266

Here is some reading on the standard classifications for Data Types (nominal, ordinal, interval, ratio):

http://www.upa.pdx.edu/IOA/newsom/pa551/lecture1.htm
http://en.wikipedia.org/wiki/Level_of_measurement

and an opposing viewpoint:
www.cs.uic.edu/~wilkinson/Publications/stevens.pdf
which cites, among other possible systems,

Mosteller and Tukey (1977 Chapter 5):

* Names
* Grades (ordered labels such as Freshman, Sophomore, Junior, Senior)
* Ranks (starting from 1, which may represent either the largest or smallest)
* Counted fractions (bounded by zero and one. These include percentages, for example.)
* Counts (non-negative integers)
* Amounts (non-negative real numbers)
* Balances (unbounded, positive or negative values).

Doing Data Science, page 23, suggests:
• Traditional: numerical, categorical, or binary
• Text: emails, tweets, New York Times articles
• Records: user-level data, timestamped event data, json-formatted log files
• Geo-based location data
• Network
• Sensor data
• Images

Also see http://stats.stackexchange.com/questions/539/does-it-ever-make-sense-to-treat-categorical-data-as-continuous

For future teachers: I was amazed to see in my daughter's 3rd grade homework a link with our Categorical/Quantitative, Discrete/Continuous discussion:

This homework sheet talks about Count, Measure, Position, and Label:
http://www.eduplace.com/math/mw/practice/3/homework/1_1.pdf

This one is amazingly similar to our activity where we talked about Nominal, Ordinal, Interval, Ratio for our start-of-semester-survey:
http://www.eduplace.com/math/mw/practice/3/enrichment/1_1.pdf

I'm not sure if it's in all such curricula--the book they're using is by Houghton Mifflin.

Dotplots

Remember that dotplots can tell us:

* S: the Shape of the distribution: (concentrated at an endpoint? Or in the middle?
* O: any Outliers or other unusual features like gaps
* C: where the data is Centered
* S: how Spread the data is (or as some call it, Variability)
so if you're writing sentences describing a dotplot, you should write at least one sentence for each of those bullet points. Remember the acronym SOCS. It’s important to do them in that order, too, because shape and outliers often influence our choice of how to measure center and spread.

For example, for a sibling-count dotplot we did one year in class:

The data is concentrated near the low end.
There are no unexpected gaps or outliers.
The center of the data is around 3.
The data is spread from 1 to 9.

A more subtle concept is “Inlier”, like an outlier in the sense that it might be a false reading, but it doesn’t fall outside the main data range. A common example is for missing data to accidentally be represented by a zero, when small numbers like zero or 1 or 2 are in fact perfectly plausible real data values.

Lexical ambiguity: making a case against spread

Jennifer J. Kaplan1, Neal T. Rogness2 and Diane G. Fisher3
Article first published online: 28 APR 2011

DOI: 10.1111/j.1467-9639.2011.00477.x
http://onlinelibrary.wiley.com/doi/10.1111/j.1467-9639.2011.00477.x/full

That article says that “variability” is a better word.

Population and Sample

First, let’s note that in statistics, a Sample almost always means more than one data value. If you poll 25 people for a project, that is a single Sample, not 25 samples. This is in contrast to how scientists often think of samples: a blood sample, or a sample from a lake or river, often makes us think of just one container of blood or water.

Doing Data Science, page 21, asks:

But, wait! In the age of Big Data, where we can record all users’ actions all the time, don’t we observe everything? Is there really still this notion of population and sample? If we had all the email in the first place, why would we need to take a sample?

And on page 25:

The way the article frames this is by claiming that the new approach of Big Data is letting “N=ALL.”
Can N=ALL?
Here’s the thing: it’s pretty much never all. And we are very often missing the very things we should care about most.

Chapter 2

Example of Sampling Frames: 3 different lists of all doctors in a country

http://www.mathematica-mpr.com/our-publications-and-findings/publications/the-results-are-only-as-good-as-the-sample-assiessing-three-national-physician-sampling-frames

optimal assignment instead of random assignment:

http://pubsonline.informs.org/doi/pdf/10.1287/opre.2015.1361

Dimitris Bertsimas, Mac Johnson, Nathan Kallus (2015) The Power of Optimization Over Randomization in Designing
Experiments Involving Small Samples. Operations Research 63(4):868-876. http://dx.doi.org/10.1287/opre.2015.1361

Confounding

Confounding vs Lurking:http://www.virmanimath.com/start-page-2012-2013/ap-stats-2012-2013/chapter-2/apstatonlineclass/confounding-and-lurking-variables

Example of confounding: Stereotypically, old people are thought of as not very good with new technology. Is that because they have lived a large number of years, or because they were born during a particular decade or two? There’s no way to disentangle those two things.

Another example: An exhibit at the Wagner farm in Glenview, IL has 3 rope/pulley systems, each trying to lift an equal weight. One is a simple pulley; the next is compound (down and up), the 3rd is even more compound (down/up/down). The ropes used are also slightly different: the most compound one uses a thinner rope. The most compound one should be the easiest to pull. [it's not, due to a lack of lubrication and some bent axles on the pulleys).

My daughter tries all 3 and decided that the diameter of the rope is what makes things easier or harder to lift.

Another example: Examining Variation in Recombination Levels in the Human Female: A Test of the Production-Line Hypothesis; Ross Rowsey, Jennifer Gruhn, Karl W. Broman, Patricia A. Hunt, Terry Hassoldemail, http://dx.doi.org/10.1016/j.ajhg.2014.06.008
and
With Gene Disorders, The Mother's Age Matters, Not The Egg's

Also, I heard this somewhere: Women who have more kids tend to have started at an earlier age than women that have fewer kids. So if you're looking for the relationship between that and breast cancer, which one is the main effect?

Imagine dropping a marble into a bucket of sand and measuring the diameter of the crater.
If you change the diameter of the impactor, you're also changing the weight (or vice versa), unless you take very great care to find marbles/balls that change density or become hollow in just the right way.
The table would look like this:
Diameter Weight DropHeight CraterSize
0.5cm 2grams 25cm 5cm
0.5cm 2grams 25cm 6cm
0.7cm 3grams 25cm 7.1cm
0.7cm 3grams 25cm 7.3cm

You could control weight separately from impactor diameter by using a non-sphere impactor, like a stack of pennies or nickels, or AA batteries. But then you'd have to be careful to control its orientation at impact--maybe have it slide down a V-shaped near-vertical channel, or suspended from a string (balanced perfectly vertically) and very still, then cut the string.

Activity

Quick activity: name that sampling method
a. Roll a die to pick a row in class, then ask each student in that row; do it twice
b. Pick a student and then every 5th student after that
c. Ask one student from each row
d. pick some students, say "you guys look like typical students"
e. throw an object, see who it hits
f. Number the students, etc.

In _______ sampling, ALL groups (strata? clusters?) are used, and SOME individuals in each are sampled.
In _______ sampling, SOME groups (strata? clusters?) are used, and ALL individuals in each are sampled.

If you’ve done Stratified sampling, how do you combine your strata results into whole-sample results? Ask me for a photocopy from Applied Statistics for Engineers and Scientists, 2^nd Edition, by Devore and Farnum.

Bias

Kate Crawford’s talk, Algorithmic Illusions: Hidden Biases of Big Data

Dotplots of Random Rectangles results, look for bias

Bias in cancer screening: Crunching Numbers: What Cancer Screening Statistics Really Tell Us, by Sharon Reynolds, http://www.cancer.gov/ncicancerbulletin/112712/page4

Bias due to question ordering: http://textbookequity.org/oct/Textbooks/Lippman_mathinsociety.pdf
page 137: A psychology researcher provides an example:
“My favorite finding is this: we did a study where we asked students, 'How satisfied are you with your life? How often do you have a date?' The two answers were not statistically related - you would conclude that there is no relationship between dating frequency and life satisfaction. But when we reversed the order and asked, 'How often do you have a date? How satisfied are you with your life?' the statistical relationship was a strong one. You would now conclude that there is nothing as important in a student's life as dating frequency.”
Swartz,Norbert. http://www.umich.edu/~newsinfo/MT/01/Fal01/mt6f01.html. Retrieved 3/31/2009

Bias in psychology studies: most undergrad students who volunteer as subjects are WEIRD (or WIRED): Western, Educated, Industrialized, Rich, and Democratic
http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=7825833

http://www.slate.com/articles/health_and_science/science/2013/05/weird_psychology_social_science_researchers_rely_too_much_on_western_college.html

Study Design
Overly Honest Methods

Does the needed sample size grow as the population grows?
Page 43 says no!!!!!!!

Here is a blank copy of Table 2.1 ; try to fill it out with “yes” and “no” entries by reasoning about each situation.

Study Description	Reasonable to generalize conclusions about group to population?	Reasonable to draw cause-and-effect conclusion?
Observational study with sample selected at random from population of interest
Observational study based on convenience or voluntary response sample
Experiment with groups formed by random assignment of individuals or objects to experimental conditions	(no entry; this row is just a header for the next 2 rows)	(no entry)
* Individuals or objects used in study are volunteers or not randomly selected
* individuals or objects are randomly selected
Experiment with groups not formed by random assignment to experimental conditions

Rating System for the Hierarchy of Evidence: Quantitative Questions

Level I: Evidence from a systematic review of all relevant randomized controlled trials (RCT's), or evidence-based clinical practice guidelines based on systematic reviews of RCT's
Level II: Evidence obtained from at least one well-designed Randomized Controlled Trial (RCT)
Level III: Evidence obtained from well-designed controlled trials without randomization, quasi-experimental
Level IV: Evidence from well-designed case-control and cohort studies
Level V: Evidence from systematic reviews of descriptive and qualitative studies
Level VI: Evidence from a single descriptive or qualititative study
Level VII: Evidence from the opinion of authorities and/or reports of expert committees

Above information from "Evidence-based practice in nursing & healthcare: a guide to best practice" by Bernadette M. Melnyk and Ellen Fineout-Overholt. 2005, page 10.
Additional information can be found at: www.tnaonline.org/Media/pdf/present/conv-10-l-thompson.pdf

Chapter 2.3: Comparative Experiments

"explanatory" variables are sometimes called "independent", and

"response" variables are often called "dependent",
but in later chapters we will learn this can cause confusion.

Blocking: means "putting into groups or blocks", rather than "obstructing".

Blocking activity: email from a friend in the Health school here at EMU:
> Dr. Ross,
> I hope your holiday went well. I have recently completed a project
> identifying some basic variables to be used in preliminary
> evaluation of gait interventions to determine whether the new
> intervention would be worth conducting an in-depth study about. The
> variables include stride length, step width, stride variability, and
> lateral displacement of the total body center of mass. As you can
> see, these variables represent some of the most basic aspects of
> stability, which is what we are always trying to improve or
> maintain, and efficiency.
>
> My question to you is: what sample size e.g. 10 trials, 20 trials, 50
> trials, would we need to take from both a control group (barefoot or
> with regular shoes) and the experimental group (the intervention) in
> order to obtain a confidence level to say that very small changes
> between the two groups is statistically significant? An example
> would be that the average lateral sway during gait was 5 mm less in
> the experimental group form the control group, is that significant
> or not?

Consider the study design here: Evidence Of Racial, Gender Biases Found In Faculty Mentoring

Or watch this video and consider how to design a study related to it:

Watch this video, called "Dove: Patches"
* If you were to design a study around this concept, what would your research question be?
* How would you design the study to answer that question?

Replication
Why do we try to do more than one trial at each level of the explanatory variable?
Imagine this data set:

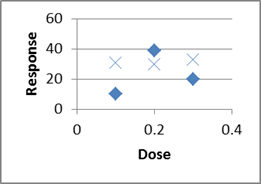
What if we had only done one trial at each dose?

Might see just the diamonds, or just the Xs, leading to two completely different ideas of the trend!

And that's just by doing two rather than one at each level!
Replication allows us to quantify the variability/uncertainty at each level.
Also, when designing, choose 3 or more X values, so we can detect nonlinearity.

Controls: Positive and Negative
Bio/Chem: when trying to detect a chemical in a sample (pollution in a lake?),
run your procedures on some known pure water (Negative Control),
and on some water with a known amount of pollutant deliberately added to it (Positive Control).

Computer Science: when testing spam-filtering software,
run it on some known non-spam ("ham")--negative control,
and on some known spam -- positive control.

What is the difference between placebo and control?
Placebos are meant to fool _people_--usually unnecessary on non-people.
While control experiments apply to people and non-people alike.
But you should still handle animals in the control group the same way (incl. surgery?)

This article is a humorous take on experimental vs observational, etc: How To Argue With Research You Don't Like,
http://www.washingtonpost.com/blogs/wonkblog/wp/2013/09/12/how-to-argue-with-research-you-dont-like/

Chapter 3

Guidelines and debate about information visualization: http://eagereyes.org/blog/2012/responses-gelman-unwin-convenient-posting and http://robertgrantstats.wordpress.com/2014/05/16/afterthoughts-on-extreme-scales/

A “Segmented Bar Chart” in our textbook is the same as a “100% Stacked” chart in Excel. If you change the widths of the bars to reflect the counts of each bar, that is called a “Mosaic” chart by most statisticians, or Fathom calls it a “Ribbon” chart. Here are some thoughts on how to make them in Excel: here and here

http://asq.org/learn-about-quality/data-collection-analysis-tools/overview/histogram2.html
includes some I haven't seen before expressed in this way:
* Edge peak. The edge peak distribution looks like the normal distribution except that it has a large peak at one tail. Usually this is caused by faulty construction of the histogram, with data lumped together into a group labeled “greater than…”

* comb distribution: In a comb distribution, the bars are alternately tall and short. This distribution often results from rounded-off data and/or an incorrectly constructed histogram. For example, temperature data rounded off to the nearest 0.2 degree would show a comb shape if the bar width for the histogram were 0.1 degree.
*heart cut distribution: like Normal but with upper and lower bounds (only selling products that fall in an acceptable range)
*dog food distribution: what's left after a heart-cut distribution (only selling products on secondary market that fall outside acceptable range)

Indian Standardized Test Histogram

A very interesting data set/set of histograms, which we would expect to have a Normal distribution like the SAT or ACT, but it's definitely non-normal in very interesting ways: (you'll need to scroll down past the description of how he collected the data in a sneaky way):
http://deedy.quora.com/Hacking-into-the-Indian-Education-System
whereas SAT data can be found at
http://research.collegeboard.org/programs/sat/data
http://research.collegeboard.org/content/sat-data-tables

Lawyer starting salaries: (and then 2007 is even worse)

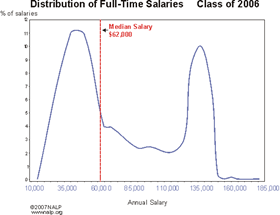
Are adult heights distributed bimodally due to male/female differences?

http://faculty.washington.edu/tamre/IsHumanHeightBimodal.pdf

http://commoncoretools.files.wordpress.com/2012/04/ccss_progression_sp_hs_2012_04_21.pdf
... two ways of comparing height data for males and females in the 20-29 age group. Both involve plotting the data or data summaries (box plots or histograms) on the same sale, resulting in what are called parallel (or side-by-side) box plots and parallel histograms. The parallel box plots show an obvious difference in the medians and the IQRs for the two groups; the medians for males and females are, respectively, 71 inches and 65 inches, while the IQRs are 4 inches and 5 inches. Thus, male heights center at a higher value but are slightly more variable.
... Heights for males and females have means of 70.4 and 64.7 inches, respectively, and standard deviations of 3.0 inches and 2.6 inches.

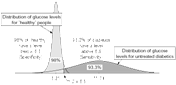
Blood Sugar Levels [note that the height of the Diabetic peak should be much smaller in the whole population, like 2% to 5%; this graph is showing two conditional distributions]

Figure 3.

Duration of pregnancy has a left-skewed histogram; doi:10.1093/humrep/det297

Birth weight and birth length probably are also left-skewed?

Where the bins start can affect the apparent shape of the histogram:http://zoonek2.free.fr/UNIX/48_R/03.html

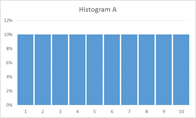
Which histogram below shows more variability, A or B? (adapted from a SCHEMATYC document)

Which time series shows more variability, A or B?

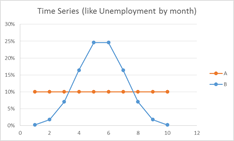
How can we address the mismatch? Focus on understanding and labeling the AXES! (I deliberately didn’t label the axes, above)

Histogram:
x = what values?
y = how many?
Time plot:
x = when?
y = what value?

data sets of quiz scores: which is more variable/harder to predict?
data set 1: 1 2 3 4 5 6 7 8 9 10; histogram looks flat
data set 2: 8 8 8 8 8 8 8 8 8 8 ; histogram has a spike

Other sample histograms from something I created for my Math 110 class. Here's the link:
http://people.emich.edu/aross15/math110/m110-coursepack-supplement-v6.docx
and just search inside the file for Histogram.

An alternative to a histogram is a Frequency Polygon; these tend to be better when showing two or more histograms on the same graph

Heart Rate Survey Data with Relative Ranks:
https://tuvalabs.com/mydatasets/d24bae4915ee4ad99a99b263f7a7143d/

Classification of Chart Types

http://www.excelcharts.com/blog/classification-chart-types/
-----------------------------------

Melanie Tory and Torsten Moller’s InfoVis 2004 paper “Rethinking Visualization: A High-Level Taxonomy” (search for it at scholar.google)
http://webhome.cs.uvic.ca/~mtory/publications/infovis04.pdf

------------------------------------------------

Choosing a Good Chart
http://extremepresentation.typepad.com/blog/2006/09/choosing_a_good.html
------------------------------------------------
a task by data type taxonomy for information visualization.
----------------
don't use rainbow colors for sequential data values:
http://www.wired.com/2014/10/cindy-brewer-map-design/
http://datascience.ucdavis.edu/NSFWorkshops/Visualization/GraphicsPartI.pdf
http://www.poynter.org/uncategorized/224413/why-rainbow-colors-arent-always-the-best-options-for-data-visualizations/
-----------------------------------------------------
a really good overview:
http://datascience.ucdavis.edu/NSFWorkshops/Visualization/
-----------------------------------------------------

Statistical Graphics for Univariate and Bivariate Data
William G. Jacoby
Quantitative Applications in the Social Sciences, #117
A Sage University Paper

page 11
from most accurate to least accurate:
A. Position along a common scale
B. Position along common, nonaligned scales
C. Length
D. Angle* [perceptual judgments abou tangles and slopes/directions are carried out with equal accuracy, so their relative ordering in this figure is arbitrary]
E. Slope, Direction* [see above]
F. Area
G. Volume
H. Fill density, Color Saturation

page 23, regarding kernel density estimates:
"In statistical terminology, narrow bandwidths produce low-bias, high-variance histograms; the density trace follows the data very closely (low bias), but the smooth curve jumps around quite a bit (high variance). Larger bandwidths are high bias and low variance because they produce a smooth density trace (low variance in the plotted values) but depart from the actual data to a more substantial degree (high bias in the graphical representation)."

[they must mean variance in the vertical height]

page 52, Construction Guidelines for Bivariate Scatterplots
mostly from Cleveland 1994
"/Make sure that the plotting symbols are visually prominent and relatively resistant to overplotting effects/. ... For example, small plotting symbols are easily overlooked. At the same time, larger filled symbols make it quite difficult to distinguish overlapping data points. For these reasons, open circles make good general-purpose plotting symbols for bivariate scatterplots.
"/Rectangular grid lines usually are unnecessary within the scale rectangle of a scatterplot/
"/The data rectangle should be slightly smaller than the scale rectangle of the scatterplot/. Otherwise, it is likely that some data will be hidden as a result of intersections between points and the scale lines....
"/Tick marks should point outward, rather than inward, from the scale lines/. ... further reduces the possibility of collisions between data points and other elements of the scatter diagram...

and then a few other, less important.

page 85, Aspect ratio and Banking to 45 degrees
https://eagereyes.org/basics/banking-45-degrees
actually argues that the original study didn't test other possibilities:
"While Cleveland et al. assumed the precision of value judgments would again decrease when going below 45º, they did not present actual data to show that.

When testing lower average slopes, Talbot et al. found that people actually got better with shallower slopes. The 45º were an artifact of the study design."

Also see:
https://eagereyes.org/section/seminal-papers
-----------------------------------------------------

Chapter 4

A puzzle to start class:
1) What value of x minimizes (x-1)^2 + (x-3)^2 + (x-8)^2 ?
2) What value of x minimizes abs(x-1) + abs(x-3) + abs(x-8) ?

(while you could use calculus on #1, you can't on #2, so I suggest just graphing both of them)

Doing Data Science, page 270: “the average person on Twitter is a woman with 250 followers, but the median person has 0 followers”

Mythbusters on Standard Deviation: testing different soccer-ball launchers, looking for consistency (dig the spreadsheet out of my email?)

Boxplots: An interesting comparative boxplot on what different hospitals charge for different blood tests: Variation in charges for 10 common blood tests in California hospitals: a cross-sectional analysis by Renee Y Hsia1, Yaa Akosa Antwi2, Julia P Nath
Figure 1: Variation in charges for 10 common blood tests in California (CBC, complete blood cell count; ck, creatine kinase; WCC, white cell count). Central lines represent median charges, boxes represent the IQR of charges, and whiskers show the 5th and 95th centile of charges for each of the 10 common blood tests.

Boxplots: variability in salaries for top 100 athletes in various US sports, from Jeff Eicher via the AP-Stats community:

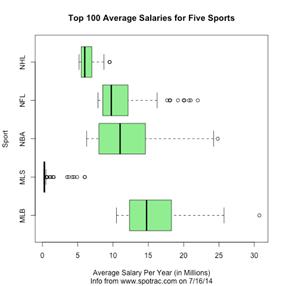
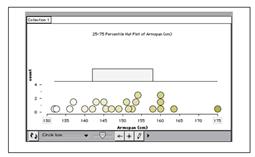
Transitioning from Dotplots to Boxplots: Hat Plots, a math-education-specific way to make the transition; shown in The Role of Writing Prompts in a Statistical Knowledge for Teaching Course by R.E. Groth (draft saved in email); Tinkerplots can do them.

Old Class Data

Here is the data that you entered this semester on your own height, in inches above 5-foot-0-inches.
We will use this in class.
Not to spoil the fun, but we will:
* make a histogram to see its general shape, in bins of width 2 inches
(use the histogram template file we've been using)
* compute the mean & SD
* compute another histogram with bin widths of 1 SD, centered on the mean
* look at the % of data points within +/- 1 SD of the mean, and then +/- 2 SD of the mean, and +/- 3 SD.

6
10.5
9
7
10
8
12
0
8
10
5
2
6
10
9.5
4 in
16.5
17
6
9
13
6
11
9
7.75
6
15
2
0.4
4 inches
6
5
14.5
12
3
5-foot-6-inches
4
11
10
11
4.75
6
12
7

8
9

12.5

8

And here's another data set, on how long it took students in one of my Math 110 classes to walk from Green Lot to Pray-Harrold, in decimal minutes:
9.4166666667
8.35
9.6
10.4666666667
10.5333333333
12.15
7.7666666667
8.1666666667
6.3666666667
6.3666666667
0.1334166667
8.2166666667
7.25
7.3333333333
22.7833333333
7.55
6.5833333333
4.45
7.1
3.7166666667
5.7166666667
11.9833333333
6.2666666667
8.6333333333
5.7
7.25
7.9666666667
7.8833333333
6.766666666

Algorithms for Computing the Mean and the Variance

Surprisingly, it can be hard to compute the mean, and especially the variance, if there is a huge amount of data, or if roundoff error is an issue. Computer science people might want to read:
http://cpsc.yale.edu/sites/default/files/files/tr222.pdf
equivalent to
Chan, Tony F.; Golub, Gene H.; LeVeque, Randall J. (1983). Algorithms for Computing the Sample Variance: Analysis and Recommendations. The American Statistician 37, 242-247. http://www.jstor.org/stable/2683386
Also:
http://en.wikipedia.org/wiki/Algorithms_for_calculating_variance

Chapter 5

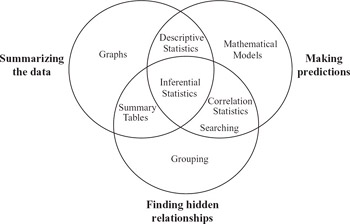
Is the main purpose of regression to make predictions? The book “Making Sense of Data, Volume I” says that statistics is for: making predictions, finding hidden relationships, and summarizing the data:

Here is another take on it: To Explain or to Predict? by Galit Shmueli

Forecasting time series data is an important statistics topic that we don’t have time to do in detail. Here is a freely available textbook chapter about it: “Chapter 16: Time Series and Forecasting”
http://highered.mcgraw-hill.com/sites/dl/free/0070951640/354829/lind51640_ch16.pdf

There are more types of regression than what we’ll learn about. See 10 types of regressions. Which one to use?

For future teachers: Unofficial TI-84 regression manual, or another site. It mentions that you need to turn on the Calculator Diagnostics to get the r and r^2 values. Do that by doing [2^nd] [Catalog] [D] [Diagnostic On] [Enter]; you should only have to do that once in the lifetime of the calculator (unless you do a full-reset?)

And, it’s important to be able to compute and plot residuals. Here are instructions for doing it on a TI-84.

also should include:
If you accidentally delete List1, then do this:
Stat -> Stat Editor -> (enter) -> (enter)

Here's an animation of what it means to have a bell-curve distribution of the residuals:
http://screencast.com/t/w7YOge93Nj
This could help in understanding the first few sheets on the pre-work for classtime

Example Plots

Here is an example heteroscedastic scatter plot: x=income, y=Expenditure on food, both in multiples of their respective mean; this is UK data on individuals, from 1968-1983

$\includegraphics[scale=0.7]{ANRfoodscat.ps}$

Here is some data on school-age children in the US, height and weight, that also shows heterskedasticity: data from http://www.nal.usda.gov/fnic/DRI/DRI_Energy/energy_full_report.pdf

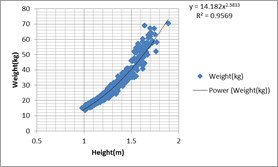
There are various tests for heteroscedasticty:http://en.wikipedia.org/wiki/Breusch%E2%80%93Pagan_test

An example Matrix of Scatterplots, from Statistical Methods in Psychology Journals:

It’s data from a national survey of 3000 counseling clients (Chartrand 1997); on the diagonal are dotplots of the individual variables, and off the diagonal there are scatterplots of pairs of variables. “Together” is how many years they’ve been together in their current relationship. What do you see in these plots?

Here’s a fun/depressing scatterplot, from OK Cupid: http://blog.okcupid.com/index.php/we-experiment-on-human-beings/

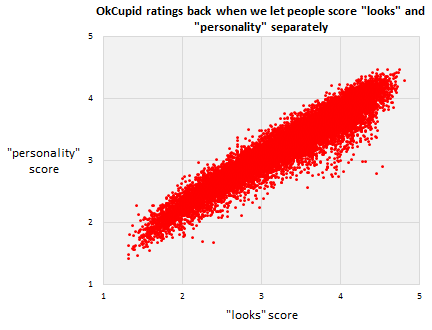
And then [in the following paragraph, what does the “less than 10%” mean, in terms of statistical things like slope, intercept, correlation coefficient, R^2, etc?]

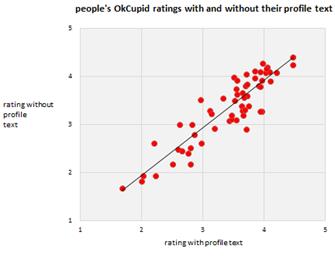
After we got rid of the two scales, and replaced it with just one, we ran a direct experiment to confirm our hunch—that people just look at the picture. We took a small sample of users and half the time we showed them, we hid their profile text. That generated two independent sets of scores for each profile, one score for “the picture and the text together” and one for “the picture alone.” Here’s how they compare. Again, each dot is a user. Essentially, the text is less than 10% of what people think of you.

Correlation and Causation

Doing Data Science, page 26:

Say you decided to compare women and men with the exact same qualifications that have been hired in the past, but then, looking into what happened next you learn that those women have tended to leave more often, get promoted less often, and give more negative feedback on their environments when compared to the men. Your model might be likely to hire the man over the woman next time
the two similar candidates showed up, rather than looking into the possibility that the company doesn’t treat female employees well. In other words, ignoring causation can be a flaw, rather than a feature. Models that ignore causation can add to historical problems instead of addressing them.... And data doesn’t speak for itself. Data is just a quantitative, pale echo of the events of our society

Also see the fantastical claims in “The End of Theory: The Data Deluge Makes the Scientific Method Obsolete” Chris Anderson, Wired, 2008

And, Statistical Truisms in the Age of Big Data by Kirk Borne

Can this data tell us anything?

http://www.deathpenaltyinfo.org/murder-rates-nationally-and-state#MRalpha

Logarithms

Grab data for infant mortality vs. gdp-per-capita from my email box?

Starbucks data: http://textbookequity.org/oct/Textbooks/Lippman_mathinsociety.pdf

Year Number of Starbucks stores
1990 84
1991 116
1992 165
1993 272
1994 425
1995 677
1996 1015
1997 1412
1998 1886
1999 2498
2000 3501
2001 4709
2002 5886
2003 7225
2004 8569
2005 10241
2006 12440
2007 15756

http://www.starbucks.com/aboutus/Company_Timeline.pdf retrieved May 2009

Like Moore’s law, but for LEDs: http://en.wikipedia.org/wiki/Haitz's_law

Range of human hearing and range of human vision:
http://eagereyes.org/blog/2012/values-worth-chart

Double-Log scales:

http://robertgrantstats.wordpress.com/2014/05/16/afterthoughts-on-extreme-scales/

http://en.wikipedia.org/wiki/Graphical_timeline_from_Big_Bang_to_Heat_Death

Regression to the Mean
http://en.wikipedia.org/wiki/Regression_to_the_mean

The Rhine Paradox, about testing for ESP

http://support.sas.com/resources/papers/proceedings10/271-2010.pdf
http://onlinestatbook.com/stat_sim/reg_to_mean/
http://books.google.com/books?id=NcFOwRCwDOQC&lpg=PA252&ots=QJJ87auCoA&dq=%22regression%20toward%20the%20mean%22%20data%20set&pg=PA251#v=onepage&q=%22regression%20toward%20the%20mean%22%20data%20set&f=false

http://isites.harvard.edu/fs/docs/icb.topic469678.files/regress_to_mean1.pdf
http://codeandmath.wordpress.com/2012/11/21/regression-to-the-mean/
http://www.stat.berkeley.edu/~bradluen/stat2/lecture12.pdf

This page points out the problem of doing repeated tests as the sample size grows--even if H0 is true, the P value will wander between 0 and 1 randomly, and if you decide to stop when it hits 0.05 you're doing something bad: http://www.refsmmat.com/statistics/regression.html

Why best cannot last: Cultural differences in predicting regression toward the mean
http://onlinelibrary.wiley.com/doi/10.1111/j.1467-839X.2010.01310.x/abstract
Roy R. Spina, Li-Jun Ji, Michael Ross, Ye Li, Zhiyong Zhang
Article first published online: 16 AUG 2010; DOI: 10.1111/j.1467-839X.2010.01310.x

Keywords: culture; lay theories of change; prediction; regression toward the mean

Four studies were conducted to investigate cultural differences in predicting and understanding regression toward the mean. We demonstrated, with tasks in such domains as athletic competition, health and weather, that Chinese are more likely than Canadians to make predictions that are consistent with regression toward the mean. In addition, Chinese are more likely than Canadians to choose a regression-consistent explanation to account for regression toward the mean. The findings are consistent with cultural differences in lay theories about how people, objects and events develop over time.

Home Run Derby. There is a popular view that players who participate in the Home Run Derby somehow "hurt their swing" and do worse in the second half of the season. This article talks about how this phenomenon can be accounted for by regression to the mean.
http://fivethirtyeight.com/datalab/the-home-run-derby-myth/

Ecological Fallacy
http://en.wikipedia.org/wiki/Ecological_fallacy

http://www.jerrydallal.com/LHSP/corr.htm

try google images for:
ecological fallacy

http://ehp.niehs.nih.gov/1103768/
Three Criteria for Ecological Fallacy
Alvaro J. Idrovo

mentions/has a diagram for

ecological fallacy
atomistic fallacy
sociologistic fallacy
psychologistic fallacy

Interpreting the Intercept

Interpreting the Intercept in a Regression Model
http://www.theanalysisfactor.com/interpreting-the-intercept-in-a-regression-model/

and the more advanced “How to Interpret the Intercept in 6 Linear Regression Examples”
http://www.theanalysisfactor.com/interpret-the-intercept/

Interpreting the Slope

http://blog.mathed.net/2012/07/settling-slope-and-constructive-khan.html

Working on her dissertation in the mid-1990s, Sheryl Stump (now the Department Chairperson and a Professor of Mathematical Sciences at Ball State University) did some of the best work to date about how we define and conceive of slope. Stump (1999) found seven ways to interpret slope, including: (1) Geometric ratio, such as "rise over run" on a graph; (2) Algebraic ratio, such as "change in y over change in x"; (3) Physical property, referring to steepness; (4) Functional property, referring to the rate of change between two variables; (5) Parametric coefficient, referring to the "m" in the common equation for a line y=mx+b; (6) Trigonometric, as in the tangent of the angle of inclination; and finally (7) a Calculus conception, as in a derivative.

[note that none of these correspond to how we view slope in statistics!]

Thinking about how to measure R^2:

eight criteria for a good R2, mentioned at http://statisticalhorizons.com/r2logistic
Kvalseth, T.O. (1985) “Cautionary note about R2.” The American Statistician: 39: 279-285

Chapter 6

Activity idea: Determine the sensitivity and specificity of the Cinderella shoe-fitting method. You will have to make some assumptions.

How can you analyze this study?
http://www.healthline.com/health-news/children-autism-risk-appears-early-in-the-placenta-042513

Autism Risk Detected at Birth in Abnormal Placentas
Written by Julia Haskins | Published April 25, 2013

Some good sensitivity/specificity examples at http://onlinelibrary.wiley.com/enhanced/doi/10.1111/1467-9639.00076/

More stuff about sensitivity and specificity:

http://www.npr.org/templates/transcript/transcript.php?storyId=407978049
http://www.npr.org/sections/money/2015/05/20/407978049/how-a-machine-learned-to-spot-depression

http://www.theatlantic.com/technology/archive/2014/05/would-you-want-therapy-from-a-computerized-psychologist/371552/

http://ict.usc.edu/prototypes/simsensei/

Chapter 6.7: Estimating Probabilities Empirically Using Simulation

http://commoncoretools.files.wordpress.com/2011/12/ccss_progression_sp_68_2011_12_26_bis.pdf

students should experience setting up a model and using simulation (by hand or with technology) to collect data and estimate probabilities for a real situation that is suﬃciently complex that the theoretical probabilities are not obvious. For example, suppose, over many years of records, a river generates a spring ﬂood about 40% of the time. Based on these records, what is the chance that it will ﬂood for at least three years in a row sometime during the next ﬁve years? 7.SP.8c

7.SP.8c Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.
c Design and use a simulation to generate frequencies for compound events.

Chapter 7

We might also have a quick quiz in class about how shifting or scaling affects the mean, variance, SD, IQR, etc., and the proper formula for the sample variance.

In class, we used the dotplot-histogram-crf-1000 sheet to investigate questions like:
* Is E[X+Y] = E[X] + E[Y] ? (yes, it always is--doesn't even need independence!)
* Is Std(X+Y) = Std(X) + Std(Y) ? (no, it basically never is!)
* Is Var(X+Y) = Var(X) + Var(Y) ? (in Excel it was close enough; with infinite trials, it's exactly true,
but we need to require that X and Y be independent, or at least uncorrelated)

Some other questions we could ask:
* Is E[X^2] = ( E[X] )^2 ?
* Is E[1/X] = 1/ E[X] ?
* Is E[X*Y] = E[X]*E[Y] ?

If you look at the 2nd multi-plotting sheet inside that file I sent, you will see a copy of what we did today, and some experiments as suggested above.

In other news, here is some advice on keeping notation straight:

http://heather.cs.ucdavis.edu/~matloff/132/PLN/ProbStatBook.pdf
Page 15:
Do not write/think nonsense. For example: the expression "P(A) or P(B)" is nonsense--do you see why? Probabilities are numbers, not boolean expressions, so "P(A) or P(B)" is like saying, "0.2 or 0.5" -- meaningless.

Similarly, say we have a random variable X. The "probability" P(X) is invalid. P(X = 3) is valid, but P(X) is meaningless.

Please note that = is not like a comma, or equivalent to the English word therefore. It needs a left side and a right side; "a = b" makes sense, but "= b" doesn't.

Similarly, don't use "formulas" that you didn't learn and that are in fact false. For example, in an expression involving a random variable X, one can NOT replace X by its mean. (How would you like it if your professor were to lose your exam, and then tell you, "Well, I'll just assign you a score that is equal to the class mean"?)

And, from Rossman and Chance, "Brief Review of Set Operations and Properties":
An event is a set, while a probability is a number.
One calculates probabilities of events (and therefore of sets), but probabilities are numbers. The following _meaningless_ statements are examples of nonsensical confusions of sets and numbers:
P(A) intersect P(B)
(P(A))'
P(1-A)
P(A+B)

Examples of _meaningful_ statements about events and probabilities include:
P(A intersect B)
P(A')
1-P(A)P(B)+P(B)

Chapter 7.5: Binomial and Geometric
first, note that an “unfair coin” is apparently nearly impossible to construct:

“You Can Load a Die, But You Can’t Bias a Coin”, Andrew Gelman and Deborah Nolan,

http://www.stat.columbia.edu/~gelman/research/published/diceRev2.pdf

How reliable is public transit? This government document says “train must stop short of an authority limit with a 0.999995 certainty”; that means it shouldn’t go past a point on the track that it isn’t allowed to go past.

Classic question: if you flip a (unfair?) coin n times, how many times will it come up heads?
The # of heads has a Binomial distribution.
2nd classic questions: if you flip a (unfair?) coin _until_ you get your first heads,
how many flips will it take?
The # of flips has a Geometric distribution.

Binomial has a fixed # flips, random #heads
Geometric has a random #flips, fixed #heads (just 1)

We already saw: P(1 energy-efficient fridges out of 3)
involved 3 different outcomes (3 trials, choose 1 E fridge)

Binomial PMF: one thing Prof. Casey has identified as
"something to know cold"!
Book uses p(x) but then also uses p for success probability--dangerous!
nCx * p^x * (1-p)^(n-x); x=0,1,..., n
Binomial PMF applet:
http://www.distributome.org/js/calc/BinomialCalculator.html

Example problems:
n=10 fair coin flips (p=1/2), P(X=5)?
0.24609375
Can use BINOMDIST(x,n,p, false) for PMF in Excel
What about P(X<=3 )?
Could do P(X=0)+P(X=1)+P(X=2)+P(X=3)
but there's a better way: binomdist using the cumulative=true option:
BINOMDIST(x,n,p,true) = P(X<=x )
0.171875
What about P(X>7)? There's no reverse-cumulative option.
Instead, say: P(X>7) is the opposite of P(X<=7: P(X>7)=1-P(X<=7)
then do 1-binomdist(7,n,p,true)
What about P(X>=7) ? Change to X>6, then use 1-P(X<=6)

How about P(3 < X <= 8)? Change to P(X<=8) - P(X<=3)

Mean & Standard Deviation:
If you flip a 60% coin 10 times, how many H do you expect? 6, of course.
So mean # of successes is E[X]=n*p
StdDev isn't so obvious. Var(X)=n*p*(1-p)
This is much more useful in Chapter 7.8, Binomial Approximations.

Geometric:
# of FLIPS until success:
P(X=x) = failure on x-1 flips, success on 1 flip = (1-p)^(x-1) * p
x=1,2,3,...
Some books call this the G1 distribution since it starts at x=1.
If we asked # FAILURES, not #FLIPS, that would start at x=0, call it G0.
(PMF is slightly different)
Wikipedia shows both types:
http://en.wikipedia.org/wiki/Geometric_distribution
P(X<=x)=1-P(X>x)=1-P(x failures at start)=1-(1-p)^x
No equivalent function in Excel.

Geometric distribution applet:
http://www.distributome.org/js/calc/GeometricCalculator.html

Book skips: Mean & Var for Geom
If each coin flip has a 1-in-10 chance of H, how many flips until H?
10 is the obvious answer, and it's right: E[X] = 1/p
Var(x)=(1-p)/p^2

Big important property of Geometric distribution: Memoryless!
If E[X]=10 and we're already on flip #8 without a H, E[#remaining flips]=10
not 10-8=2

Things that might have a Geometric distribution: # children per family? #dogs or #cats per family? #pets per family? #people per car? #marriages per person? # officers at each rank of the military (2nd Lt, Lt, captain, major, lt. Colonel, Cl, 1-star general, etc.), or similarly for enlisted? #dancers left in SYTYCD callbacks? (data in my email box)

Chapter 7.6: Normal Distribution
If you want to see the formula for the bell curve, visit
http://en.wikipedia.org/wiki/File:10_DM_Serie4_Vorderseite.jpg
We hardly ever use that formula in Stats class, though, other than to graph it and shade in some areas so we can see what we are doing.

Start with Standard Normal: mean=0, stddev=1
This is so special it gets its own letter: z instead of x
(we already calculated z-scores; it's not a coincidence!)

Cumulative Distribution Functions: this applet draws the cumulative area under the curve:

https://www.desmos.com/calculator/auhxppbg8c

Or a more old-fashioned applet, http://www.flashandmath.com/mathlets/calc/antplot/antplot.html
1/sqrt(2*pi)*e^(-x^2/2)
y range on f(x) to [0,0.4]
x range on f(x) to [-3,3]
F(-3) = 0.0013

It's hard to compute something like P(Z<=1) from scratch, so we use tables or Excel formulas.
Shade area on bell curve for Z<=2, look up in table,use Excel formula =normdist(2,0,1,true)
And highlight on CDF graph.
Now try for P(-0.5 < Z < 0.5)

Now backwards: what z cutoff gives P(Z<=z) = 0.80 ?
And double-backwards: what z cutoff gives P(-z < Z < z)=0.95 ?

Non-Standard distributions: translate to z-scores and back.
On the graph printouts, write in x values next to z values.
Speeds on a particular road average 40 mph, sigma=5
What % of speeds are under 45?
What % of speeds are between 30 and 50 ?

Normal Distribution applet:
http://www.distributome.org/js/calc/NormalCalculator.html
(the autoscaling makes it near-worthless because it always looks the same,
but that's kind of the point!)

Excel: for finding Pr from cutoff, =normdist(cutoff, mean, std, true)
For finding cutoff from Pr, use =norminv(prob, mean, std )

Chapter 7.7: Checking for Normality, and Normalizing Transformations

Big initial notice: don't sweat the details of the formulas here, since each book and software package does things a little differently.

Normal probability Plot, also called Q-Q (Quantile-Quantile) plot for Normal

Basic idea: could make a CRF plot directly from data (no binning), then overlay a NormalCDF plot. But it's hard to tell how well two CURVES match. So we plot x=exact Normal quantiles, y=data quantiles, which should make a straight line if the distribution is Normal.

Show Q-Q plot in existing Excel file; don't construct by hand in class!

If the data isn't Normal, sometimes we transform it
(take sqrt, cubert, or log) to see if that makes it more normal.
Some people say that stock market returns are normal once you take logs:

Ln(price today / price yesterday)
This is called a LogNormal distribution.

Read in the book: using correlation coefficient to decide if it's reasonably close to linear.

Doing Data Science, page 31, figure 2-1, shows a collection of various distributions. They left out highly-skewed distributions like Pareto, and Gamma or Weibull with CV > 100% (so skewed their PDF graph has a vertical asymptote at x=0, rather than touching the y-axis).

Chapter 7.8: Approximating Binomial with Normal

Important intuition:
We noticed that the Binomial distribution often looked bell-curve-shaped.
So we could approximate Binomial probabilities with Normal probs.
Match the mean & the StdDev.
mean = n*p, stddev = sqrt(n*p*(1-p) )

P( a < Binom(n,p) < b ) approx= P( a < Normal < b)

For instance: flip 1000 times with p=0.4
mean=1000*0.4=400, std=sqrt(1000*0.4*0.6)=
15.4919333848297
Pr( Binom within +/- 15 of mean of 400?)

Exact: =binomdist(400+15,1000,0.4,true)-binomdist(400-15,1000,0.4,true)
Google Docs spreadsheet gives an overflow error:
#NUM!
name-brand Excel gives
0.666757849
Normal Approximation: =normdist(400+15,400,15.49,true)-normdist(400-15,400,15.49,true)
0.667138730035761

Less-important, detail-oriented stuff: using < versus <=, and the Continuity Correction.

binomial approximations applet: http://www.jsc.nildram.co.uk/examples/sustats/normalapproximations/NormalApproximationsApplet.html

Chapter 8: Sampling Distributions

The answer to problem 8.25 (interracial couples) in the back of the book has a typo. It lists the mean of phat as 0.65 or 65%, when it should be 0.07 or 7% as stated in the problem for the population. The 65% comes from the answer to the previous problem, 8.24--it was a copy/paste error.

Is N=1 useful?

Doing Data Science, page 26:

At the other end of the spectrum from N=ALL, we have n=1, by which we mean a sample size of 1. In the old days a sample size of 1 would be ridiculous; you would never want to draw inferences about an entire population by looking at a single individual. And don’t worry, that’s still ridiculous. But the concept of n=1 takes on new meaning in the age of Big Data, where for a single person, we actually can record tons of information about them, and in fact we might even sample from all the events or actions they took for example, phone calls or keystrokes) in order to make inferences about them. This is what user-level modeling is about).

But it's false that we wouldn't draw inferences about an entire population based on n=1. n=1 is infinitely better than n=0, if you have no prior information.

Examples where n=1 is important:
A new restaurant opens. You haven't read anything about it, but your friend tried it and hated it (or liked it).
More serious: In a Phase 1 (safety) medical trial, suppose that the first patient you give it to has a horrible reaction and dies immediately. Would you say “well n=1 doesn’t mean anything, let’s give it to the next person”?

E[X_1]= mu, no matter what.

n=1 lets you estimate the mean but not the spread.
n=2 lets you estimate the spread (very poorly, but at n=1 it's impossible).
n=3 lets you estimate the skew (again, very poorly, but at n=2 it’s impossible to estimate skew)
n=4 lets you estimate the kurtosis (again, very poorly…)

Effect of increasing sample size on a boxplot: Start with a simple box-and-whisker plot, perhaps 50 data points, roughly symmetric. What will it look like if we take 10-times as much data?

The box edges will:

a) not systematically change

b) move much closer to the median

c) move farther away from the median

The whiskers will:

a) not systematically change

b) get longer

c) get shorter

Class examples

We'll use the “billionaire-dotplot-histogram-crf-1000” in file in class.

We'll also use these applet pages:
http://www.stat.auckland.ac.nz/~wild/WPRH/index.html

Sampling distribution: (the javascript version, no java problems!)
http://onlinestatbook.com/stat_sim/sampling_dist/index.html

Headlines about how charter schools are the best and the worst:
http://bridgemi.com/2015/02/charters-flood-top-and-bottom-of-academic-state-champs-rankings/
http://bridgemi.com/2014/01/searchable-database-academic-state-champs/

A very good article on why it’s important that the standard error falls inversely with sqrt(n) :

http://nsmn1.uh.edu/dgraur/niv/TheMostDangerousEquation.pdf

Below, I'm including some text about sampling distributions from a different book. Please read it.

from "Workshop Statistics, 4th Edition" by Rossman and Chance:
Topic 13: Sampling Distributions: Proportions
page 278

Watch Out!

*The concept of sampling distribution is one of the most difficult statistical concepts to firmly grasp because of the different "levels" involved. For example, here the original observational units are the candies, and the variable is the color (a categorical variable). But at the next level, the observational units are the samples, and the variable is the proportion of orange candies in the sample (a quantitative variable). Try to keep these different levels clear in your mind.

[to Math 360 students: we will see this categorical/quantitative split in Chapter 8.3; it's not so apparent in Chapter 8.1 and 8.2]

* It's essential to distinguish clearly between parameters [math 360: our book calls them population characteristics] and statistics. A parameter is a fixed numerical value describing a population. Typically, you do not know the value of a parameter in real life, but you may perform calculations assuming a particular parameter value. On the other hand, a statistic is a number describing a sample, which varies from sample to sample if you were to repeatedly take samples from the population.

* Notice that the Central Limit Theorem (CLT) specifies /three/ things about the distribution of a sample proportion [and also about a sample mean]: shape, center (as measured by the mean), and spread (as measured by the standard deviation). It's easy to focus on one of these aspects and ignore the other two. As with other normal distributions, drawing a sketch can help you to visualize the CLT.

* Ensure that these conditions hold before you apply the CLT: the sample needs to have been chosen randomly, and the sample size condition requires that n*pi>=10 and n*(1-pi)>=10 [math 360: we say n*p>=10 and n*(1-p)>=10]. ... it's the normal shape that depends on this condition. The results about the mean and standard deviation hold regardless of this condition.

* Notice that the sample size, relative to the value of the population parameter, is a key consideration when prediction whether or not the sampling distribution will be approximately normal. However, changing the sample size is in no way changing the parameters or shape of the categorical population distribution!

* As long as the population size is much larger than the sample size (say, 20 times larger), the /population/ size itself does not affect the behavior of the sampling distribuiton. This sounds counterintuitive to most people, because it means that a random sample of size 1000 from one [US] state will have the same sampling variability as a random sample of size 1000 from the entire country (with the same population proportion). But think about it: if chef Julia prepares soup in a regular-sized pot and chef Emeril prepares soup in a restaurant-sized vat, you can still learn the same amount of information about either soup from one spoonful. You don't need a larger spoonful to decide whether you like the taste of Emeril's soup.

* As we've said before, try not to confuse the sample size with the number of samples. The sample size is the important number that affects the behavior of the sampling distribution. In practice, you only get one sample. We have asked you to simulate a large number of samples only to give you a sense for how sample statistics vary under repeated sampling; we have tried to ask for enough samples (typically 500 or 1000) to give you a sense of what would happen in the long run. In fact, now that you know the Central Limit Theorem's description of how sample proportions vary under repeated sampling, you no longer need to simulate taking many samples from the population.[AMR1]

Simpson’s Paradox supplemental reading:

From Jeff Witmer at Oberlin: http://new.oberlin.edu/dotAsset/1801848.ppt

From Tom Moore at Grinnell: http://www.math.grinnell.edu/~mooret/reports/SimpsonExamples.pdf

And an article that’s very good for pre-service teachers: Representations of Reversal: An Exploration of Simpson's Paradox by Lawrence Mark Lesser, http://www.statlit.org/PDF/2001LesserNCTM.pdf

Also, this article discusses the possibility of a “Double Simpson’s Paradox”, and then it turns out that such a thing is impossible: Friedlander, Richard, and Stan Wagon. "Double Simpson's Paradox." Mathematics Magazine 66 (October 1993): 268

Other related paradoxes: Lord's Paradox ; Kelley's Paradox and Lord's Paradox

Simpson's Paradox, Lord's Paradox, and Suppression Effects are the same phenomenon – the reversal paradox, Yu-Kang Tu, David Gunnell and Mark S Gilthorpe

Help on Problem 8.14:

A student asked me for more guidance on homework 8 #8.14, where I ask you to draw a picture of the sampling distribution (on paper, or however you want--no need to turn it in).

To give some examples of what I was imagining, I went and drew curves from our class examples (rather carefully) and they are in the file “m360-sampling-distribution-drawings.xls” . You don't have to do them this carefully at all--you could just freehand them.

I added an illustration of which probabilities we were computing by freehanding stuff in Microsoft Paint. Again, you don't have to do that.

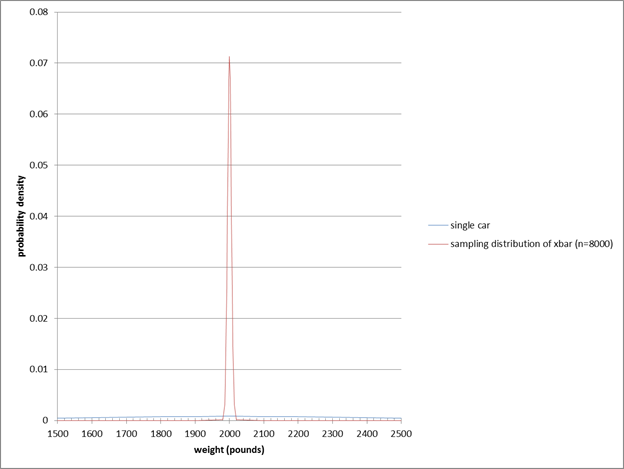
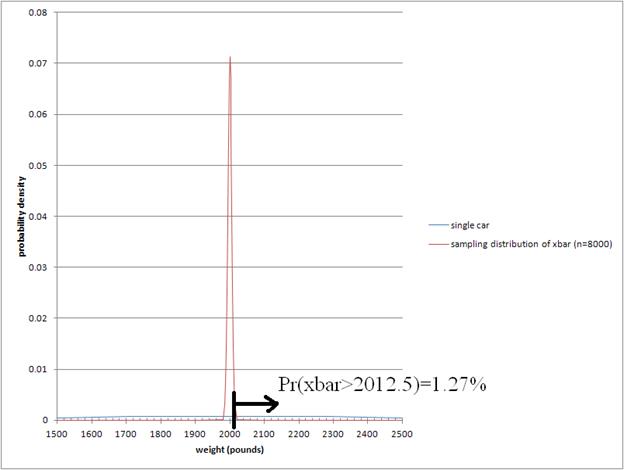
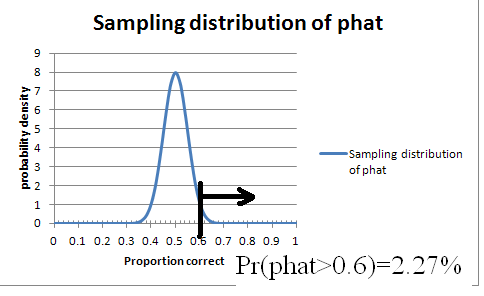
Chapter 9

First, we'll use the "estimators" file that is attached.

Later, we'll use this applet:
http://lock5stat.com/statkey/bootstrap_1_cat/bootstrap_1_cat.html

Near the end of class, we'll use:
http://www.rossmanchance.com/applets/ConfSim.html
(this applet uses JavaScript instead of Java, so it should work on more machines)

Algebraic proof of why we use n-1 in sample variance:
http://pascencio.cos.ucf.edu/classes/Methods/Proof%20that%20Sample%20Variance%20is%20Unbiased.pdf
http://en.wikipedia.org/wiki/Bessel%27s_correction

Khan Academy videos and applets on use of n-1 in sample variance:
https://www.khanacademy.org/math/probability/descriptive-statistics/variance_std_deviation/v/simulation-showing-bias-in-sample-variance
https://www.khanacademy.org/math/probability/descriptive-statistics/variance_std_deviation/v/another-simulation-giving-evidence-that--n-1--gives-us-an-unbiased-estimate-of-variance

Confidence Intervals Applet from Peck/Olsen/Devore:

http://www.thomsonedu.com/statistics/book_content/0495118737_peck/misc/SS/Applets/applets2/PeckConfsim.html

Bias vs Variance Tradeoff

* how much historical information to include when analyzing things like inflation, stock market, population growth, etc.
- high variance, low bias: only include recent info
- low variance, high bias: include lots of history, even though conditions might have changed (new laws about how government deals with finance markets, etc.)

* doing assessment on a class with only a few math majors like Calculus I:
- high variance, low bias: only test the math majors
- low variance, high bias: test everyone, hoping that the non-math-majors are reasonably similar to math majors
(but then could you look at the difference of means between math & nonmath to unbias it? But then you're just using n=#math majors again)

* Measuring pulse after exercise:
- high variance, low bias: take pulse in 10-second increments
- low variance, high bias: take pulse in 60-second increments (even though you know pulse rate is falling during that time; if it were falling linearly that wouldn't be biased, but if it's falling like exponential decay then it's biased low compared to the pulse rate at the middle of the interval, by Jensen's theorem)

* computing average waiting time or #-in-system in a queueing system with warmup:
- high variance, low bias: cut out the warmup data before averaging
- low variance, high bias: include warmup data in the average
But, Winifred Grassmann paper that says it's still better to include the warmup period (just in Markovian case?)

* maybe; using median/Ln(2) to estimate the mean of an Exponential distribution?
- but is that even biased?

http://web.engr.oregonstate.edu/~tgd/classes/534/slides/part9.pdf

Models that fit the data poorly have high bias:
inflexible models such as linear regression, regression stumps

Models that can fit the data very well have low bias but high variance:
flexible models such as nearest neighbor regression, regression trees

http://www.cs.cornell.edu/courses/cs578/2005fa/CS578.bagging.boosting.lecture.pdf

Good article on more data vs better models, bias vs variance tradeoff:
http://www.kdnuggets.com/2015/06/machine-learning-more-data-better-algorithms.html

Also, the Norvig article The Unreasonable Effectiveness of Data (attached)

Caltech lectures on machine learning; this one is about bias vs variance:

https://www.youtube.com/watch?v=zrEyxfl2-a8&hd=1

Confidence Intervals Other Than 95%

One thing that you could figure out for yourself, but we might as well highlight here, is how to compute the critical value for confidences other than 95%. Remember that we want the z-value that gives a 95% central probability, which means 5% in the tails, or 5%/2 in each tail. To turn a probability into a z-value, we use NormInv. And we want 5%/2 in the left tail; this will give us a negative z value, but we want a positive z value. So we can use
abs(norminv(0.05/2,0,1))
or
abs(norminv( (1-0.95)/2, 0, 1)
The 0 and 1 make it a Standard Normal (mean 0, SD 1) so we get a truly standard z value.

There are other ways to do it, which I list below. You could read through them and try to figure out how each works, if you're the kind of person who likes having multiple ways to do something.

Other ways:
-norminv(0.05/2,0,1) [note: not 1-norminv, just -norminv]
norminv(1-0.05/2,0,1)
norminv(0.95 + 0.05/2,0,1)

Common measures of Effect Size

difference of means
% difference of means
Cohen's d or Cohen's g : (xbar1 - xbar2)/s , not using sqrt(n)

difference of risk
relative risk
Odds Ratio
[think about 10% becoming 15%, a 5 pctg. pt. change but a 50% increase; compare to 1-to-1million vs 1.5-to-1million ]

r
R^2
slope

Chapter 10

Big-Picture skeptical discussion on use of p-values and Hypothesis Testing

Big disclaimer: almost everything in science uses the basic idea of this chapter, but it has fundamental problems that most statisticians acknowledge!

http://www.americanscientist.org/issues/feature/2014/6/the-statistical-crisis-in-science/1

One article talked about a different measure of significance as “a p-value you can’t buy”—the idea being that you can always get a better p-value by spending more money to take a bigger sample.

How to kill your grandmother with statistics, the problem with Null Hypothesis Significance Testing (NHST is okay “if all results are equally good or bad to you, and you have no prior information”)

http://golem.ph.utexas.edu/category/2010/09/fetishizing_pvalues.html

The Earth Is Round ( p<0.05), by Jacob Cohen, https://labs.psych.ucsb.edu/janusonis/skirmantas/cohen1994.pdf

http://quomodocumque.wordpress.com/2013/05/13/tantalisingly-close-to-significance/#comment-16547

Chapter 11.9, page 230 of:
http://heather.cs.ucdavis.edu/~matloff/132/PLN/ProbStatBook.pdf
What's Wrong with Significance Testing and What to Do Instead

book: The Cult of Statistical Signicance, by S. Ziliak and D. McCloskey

quotes about HT: http://www.indiana.edu/~stigtsts/quotsagn.html

Leland Wilkinson and the Task Force on Statistical Inference: Statistical Methods in Psychology Journals

An article from the journal Nature: Scientific method: Statistical errors
P values, the 'gold standard' of statistical validity, are not as reliable as many scientists assume.

"Why Most Published Research Findings Are False" (Ioannidas)
"Most Published Research Findings Are False—But a Little Replication Goes a Long Way"

Key words: p-hacking, or p-value hacking

http://www.statsblogs.com/2015/05/29/john-bohannons-chocolate-and-weight-loss-hoax-study-actually-understates-the-problems-with-standard-p-value-scientific-practice/?utm_source=feedburner&utm_medium=feed&utm_campaign=Feed%3A+statsblogs+%28StatsBlogs%29

Lack of statistically significant difference isn’t the same as proving no difference: http://www.nytimes.com/2015/02/06/upshot/no-more-running-probably-isnt-bad-for-you.html?_r=2&abt=0002&abg=1

https://www.youtube.com/watch?v=5OL1RqHrZQ8
Dance of the P-Values by Geoff Cumming

The New Statistics: Why and How
Geoff Cumming
http://pss.sagepub.com/content/25/1/7.full
(includes a graph of 2 groups with their CI, and a CI for the difference like we'd want in chapter 11 2-sample t-test for difference of means)
[ other graph ideas at http://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.1002128 ]

Against null-hypothesis significance testing (Also from APA, ironically!)
Kline, R.B. (2004) Beyond Significance Testing. Reforming Data Analysis methods in Behavioral Research
Washington, D.C.: APA Books
chapter 3: What's Wrong with Statistical Tests--And Where Do We Go From here
http://www.apastyle.org/manual/related/kline-2004.pdf

There’s Life Beyond .05
Embracing the New Statistics
Share on twitterShare on printShare on emailShare on facebookMore Sharing Services
By Geoff Cumming
http://www.psychologicalscience.org/index.php/publications/observer/2014/march-14/theres-life-beyond-05.html

http://lesswrong.com/lw/g13/against_nhst/
http://www.indiana.edu/~kruschke/BEST/
http://lesswrong.com/lw/f7t/beyond_bayesians_and_frequentists/

Phrasings

WE NEVER SAY what the probability of H0 itself is!
That's the Frequentist way. Bayesians are happy to talk about it.

In a criminal trial, we (the people) want to show strong evidence of guilt, so Ha = guilty; then H0 = not guilty, which is not the same as innocent. (though in the French system it's the opposite!)

If the data is unlikely under the supposition of H0, then we "reject H0" and accept Ha.
BUT if the data isn't particularly unlikely (supposing H0), then we NEVER NEVER NEVER "accept H0"; we just fail to reject it. In a criminal trial, we don't declare them innocent, we just fail to prove that they are guilty.

Hypotheses are about things we DON'T know, like mu or p or sigma. There's no point having a hypothesis about something we DO know, like xbar or phat.

Often we reason this way:
I want to show my product is better than the specification:
Ha : my quality (population % good) > specified value of p
So what's the opposite?
H0: my quality (population % good) <= that specified value fo p
BUT: 1) to assume H0 is true we need a specific value, not just <=,
AND the most conservative thing to do is let it be as close as possible to what I'm trying to show: =specified value rather than <specified.
So while H0 often would naturally be a <= or >= we state & treat it as an =

We can never show that two things ARE equal, just fail to show that they aren't.
(but maybe we just didn't collect enough data)

Application idea: http://en.wikipedia.org/wiki/Demining Mine flail effectiveness can approach 100% in ideal conditions, but clearance rates as low as 50–60% have been reported.[16] This is well below the 99.6% standard set by the United Nations for humanitarian demining.[6]
[6] http://www.mech.uwa.edu.au/jpt/demining/info/what-is.html

Which tail should you pick? Depends on what you're trying to prove:
my product is better than the standard
this product is worse than the standard.
Example 10.3 is very good!
But note that we might be willing to use the new treatment even if it is provably less effective than the old, as long as it's a lot cheaper or has less side effects. BUT you have to decide before you see the data; if you let your choice be influenced by the data, you won't hit your confidence/significance level!

Consider Oscar Pistorious (before his murder trial), or any other para-olympics athlete with prosthetics; to prove that they should be allowed in the ordinary olympics, should they prove that they aren't better than others? or prove they aren't worse? Or two-sided?

Wikipedia page on: Testing hypotheses suggested by the data
http://en.wikipedia.org/wiki/Testing_hypotheses_suggested_by_the_data

One-sided (one-tailed) vs Two-sided (two-tailed) tests:
If Ha is "this population is better" than a standard, use > of course,
or use < if Ha is "this population is worse" than a standard.
Sometimes we just want to show it's _different_ than a standard:
Ha: p not equal to some standard value. This is called a two-sided or two-tailed test.
Two-sided is the default if you can't decide; it's safer because its cutoff values are farther away from the hypothesized value.

What if we really want to show that the mean IS equal to something, rather than not-equal?
There's no way to do it with hypothesis testing. Confidence Intervals to the rescue!

Page 585, Example 10.7: null hypothesis implicitly includes mu<15, but book says includes mu>15 (am I right on that?)

Here is one way of laying out the 9-step process in Excel, all in one row (or actually two, one for headings and the other for numbers/calculations):

definition H0 value of p Ha alpha pop. Size (approx) n #successes phat n*p n*(1-p) sample/pop SE of phat ASSUMING H0 test statistic z p value decision

Catch Phrases

"P-value low, the null must go; P-value high, the null must fly"

another phrase:
http://blog.gembaacademy.com/2007/02/27/hypothesis-testing/
The null hypothesis is the statement of no change. I always remember it like this, “Ho hum… there is no difference here.”
Conversely, the alternative hypothesis is the statement of change. Just remember, “a Ha, there is a change!”

“If P is low, Ho must go. If P is high, Ho can fly.”

Costs of Type I vs Type II error

http://www.kdnuggets.com/2014/08/interview-pedro-domingos-winner-kdd-2014-data-science-innovation-award.html

has a quote from a prominent (award-winning) researcher: “most classifiers assume all errors are equally costly, but in reality this is seldom the case. Not deleting a spam email will cost a fraction of a second of your attention, but deleting an email from your boss could cost you your job...The bottom line is, you want to use either a natively cost-sensitive learner or an algorithm like MetaCost, or your system will be making a lot of costly mistakes.”

Here’s another opinion: Type II errors are the ones that get you fired, http://punkrockor.wordpress.com/2014/02/04/type-ii-errors-are-the-ones-that-get-you-fired-the-atlanta-edition/

And, another way of looking at errors:

Type S: an error in the sign of an effect
Type M: an error in the Magnitude of an effect

http://www.tandfonline.com/doi/full/10.1080/09332480.2013.868758#.UuFI0_Qo5ok

Type III (and IV) error
http://en.wikipedia.org/wiki/Type_III_error#Type_III_errors

Power

By convention, we use an alpha (α) level of .05 and a power of .80 in social science research.

http://www.amstat.org/education/stn/pdfs/STN85.pdf

Also has a table of required sample size to achieve given alpha and power=0.80 with Cohen's d set to small, medium, large.

Things I Have Learned (So far); Jacob Cohen; 1990
http://www.stats.org.uk/statistical-inference/Cohen1990.pdf
says:
"for a two-independent-group-mean comparison with n=30 per group at the sanctified two-tailed 0.05 level, the probability that a medium-sized effect would be labeled as significant by the most modern methods (a t test) was only 0.47. Thus, it was approximately a coin flip whether one would get a significant result, even though, in reality, the effect size was meaningful)”

“To minimize the maximal expected risk (Neyman-Pearson), the ratio of alpha to beta should be the inverse of the ratio of type-I to type-II risks. Hence, If type-II errors are 2x more severe than type-I errors (as one might argue in a - non-aviation - "pilot" study), one might convincingly argue, e.g., for level/power of .20/.90. This get's you about the same sample size as the "conventional" (aka unjustified) .05/80 ratio.”-- Knut Wittkowski; Head, Dept. Biostatistics, Epidemiology, and Research Design; The Rockefeller University, via an ASA email list.

How to Read Education Data Without Jumping To Conclusions

http://www.theatlantic.com/education/archive/2014/07/how-to-read-education-data-without-jumping-to-conclusions/374045/

One of the less-obvious items:
3. Does the study have enough scale and power?

Desmos demonstration of power versus significance:
https://www.desmos.com/calculator/qa1zy0yd12
and a way to animate the tradeoff between significance and power: (click the Play button on the "c" slider):
https://www.desmos.com/calculator/gyej6qxnlc

Reading Prompts for a Concept-based quiz on CI and HT

Very little calculation is required for this quiz; it's more about phrasing.

Here are the situations that will be part of the quiz. Each situation will be followed by 5 options, and you will chose 1 of those 5.

1. Only 33% of students correctly answered a difficult multiple-choice question on an exam given nationwide. Professor Chang gave the same question to her 35 students, hypothesizing that they would do better than students nationwide. Despite the lack of randomization, she performed a one-sided test of the significance of a sample proportion and got a P-value of 0.03. Which is the best interpretation of this P-value?

2. Researchers constructed a 95% confidence interval for the proportion of people who prefer apples to oranges. They computed a margin of error of +- 4%. In checking their work, they discovered that the sample size used in their computation was 1/4 of the actual number of people surveyed. Which is closest to the correct margin of error?


3. A survey of 200 randomly selected students at a large university found that 105 favor a stricter policy for keeping cars off campus. Is this convincing evidence that more than half of all students favor a stricter policy for keeping cars off campus?


4. In college populations, the annual incidence of infectious mononucleosis has been estimated to be as many as about 50 cases per 1000 students. A university student health service took a survey of students to test whether the rate of mononucleosis on their campus is different from this national rate. With alpha=0.05, they rejected the null hypothesis. Which is the best interpretation of "alpha=0.05" in this context?
Source: www.aafp.org/afp/20041001/1279.html


5. In a pre-election poll, 51% of a random sample of voters plan to vote for the incumbent. A 95% confidence interval was computed for the proportion of all voters who plan to vote for the incumbent. What is the best meaning of "95% confidence"?


6. Sheldon takes a random sample of 50 U.S. housing units and finds that 30 are owner occupied. Using a significance test for a proportion, he is not able to reject the null hypothesis that exactly half of U.S. housing units are owner occupied. Later, Sheldon learns that the U.S. Census for the same year found that 66.2% of housing units are owner occupied. Select the best description of the type of error in this situation.

Chapter 11

Here's a video that is meant for a different textbook, but it's still a good overview of what we've been looking at recently. It's interesting to note that their requirements for tests are slightly different: n>40 instead of n>30 for non-normal data, and n*p>15 in some cases, >10 in others, and >5 in some!

http://bcs.whfreeman.com/statsportal/bps4e/stattutor/chapter%2022/Inferences%20about%20Variables%20Part%20III%20Review.swf

Post-Minus-Pre vs Regression

I had discussed the idea of regression instead of doing post-pre subtraction with a colleague a few years ago. Then she discussed it with someone else, who emailed us this suggestion:
… the statistical analysis may have more nuance than a simple difference of scores. Some people may say that the gain score should be adjusted by the pre-test, for example. See:

http://wiki.math.yorku.ca/index.php/Statistics:_Gain_scores_vs._residualized_gain_scores

That page talks about ANCOVA (Analysis of Covariance), which is a more advanced topic than our course has time to tackle (we don't even get to the simpler version called ANOVA). So don't worry about the details on that, just think about the general experimental (/observational in some cases) setup and the questions we're asking. Also see Use of covariates in randomized controlled trials
GERARD J.P. VAN BREUKELEN and KOENE R.A. VAN DIJK

Testing by Overlapping Confidence Intervals

Wouldn’t it be great if we could skip a 2-sample t-test and just see if the confidence intervals for the two means overlap? It turns out, yes and no:

http://wise.cgu.edu/downloads/CI_Overlap_Instructions.pdf
http://iase-web.org/documents/papers/icme10/Schield.pdf
http://www.cscu.cornell.edu/news/statnews/stnews73.pdf
http://www.statlit.org/pdf/2013-Schield-Confidence-Intervals-Display-6up.pdf

Schenker, N., and Gentleman, J.F. (2001). On Judging the Significance of Differences by Examining the Overlap Between Confidence Intervals. The American Statistician, 55(3): 182–186.

A Cautionary Note on the Use of Error Bars, by John R. Lanzante

What Data Scientists call A/B Testing

Data Science people use the term A/B testing for what statistics people call a 2-sample t-test or z-test, or sometimes more than 2 samples (in which case statisticians use ANOVA or Chi-squared tests):

http://en.wikipedia.org/wiki/A/B_testing

http://blog.optimizely.com/2010/11/29/how-obama-raised-60-million-by-running-a-simple-experiment/
How Obama Raised $60 Million by Running a Simple Experiment
By Dan Siroker

We tried four buttons and six different media (three images and three videos). We used Google Website Optimizer and ran this as a full-factorial multivariate test which is just a fancy way of saying we tested all the combinations of buttons and media against each other at the same time. Since we had four buttons and six different media that meant we had 24 (4 x 6) total combinations to test. Every visitor to the splash page was randomly shown one of these combinations and we tracked whether they signed up or not.
----------------------------------
http://www.marketingexperiments.com/blog/general/email-marketing-how-ab-testing-raised-500-million-for-obama-for-america.html
-------------------
http://kylerush.net/blog/optimization-at-the-obama-campaign-ab-testing/
Obama campaign: a/b testing
Dec 12, 2012

Optimization was the name of the game for the Obama Digital team. We optimized just about everything from web pages to emails. Overall we executed about 500 a/b tests on our web pages in a 20 month period which increased donation conversions by 49% and sign up conversions by 161%. As you might imagine this yielded some fascinating findings on how user behavior is influenced by variables like design, copy, usability, imagery and page speed.

What we did on the optimization team was some of the most exciting work I've ever done. I still remember the incredible traffic surge we got the day the Supreme Court upheld Obamacare. We had a queue of about 5 ready-to-go a/b tests that would normally take a couple days to get through, yet we finished them in just a couple hours. We had never expected a traffic surge like that. We quickly huddled behind Manik Rathee—who happened to be the frontend engineer implementing experiments that day—and thought up new tests on the fly. We had enough traffic to get results on each test within minutes. Soon our colleagues from other teams gathered around us to see what the excitement was about. It was captivating to say the least.

Resampling

Some examples where resampling works but t-tests don’t [includes Fun data sets, too:
* telling girl scouts their cookie sales will help fund a trip to Disneyland
* time to back out of a parking spot when there is/isn't someone waiting.]

Chapter 12

Here is a chi-squared test for independence calculator:
http://turner.faculty.swau.edu/mathematics/math241/materials/contablecalc/

A point of view that sometimes bar charts are better than mosaic plots:
http://www.perceptualedge.com/articles/visual_business_intelligence/are_mosaic_plots_worthwhile.pdf

On the NPR radio show "On The Media" on 2014-08-17,
http://www.onthemedia.org/story/cameras-interrogation-room/
UCLA law professor Jennifer Mnookin was talking about the use of videotaping in police interrogation rooms:
"We do know certain red flags that may be associated with false confessions. In many of the known false confession cases , the interrogations were unusually long. But at the same time, lots of true confessions may come after long interrogations."

What kind of thinking is that?

In class:
Let's see if we can gather some binomial data. Let's use families with 2 kids (if your family has more than 2, just consider the first 2).
Go here (but remove the REMOVETHIS first)
https://docs.gooREMOVETHISgle.com/forms/d/1NBh5OpRoXPXQMy1VcpjTIuRKeQ5tryEFI3sIMnAZ5b0/viewform
and enter either GG, GB, BG, or BB.
---------------------------------
Chi-squared stuff:

Desmos calculator that I made to show how the Chi-squared distribution changes as DoF increases:
https://www.desmos.com/calculator/swmkwk8fyx

Distributome:
http://www.distributome.org/js/calc/ChiSquareCalculator.html

My excel sheet with a slider; might work only on PCs rather than Macs. Also, requires you to enable macros, which is dangerous in general but probably safe for this one file.
-------------------------------------

Mythbusters checked if yawns are contagious: The results:

25%, 4 out of 16, who were not exposed to a yawn, yawned while waiting. Call this the non-yawn group.
29%, 10 out of 34, who were exposed to a yawn, yawned. Call this the yawn group.

Is it a statistically significant difference? How small could the sample be to be able to detect a 25% vs 29% difference?

-------------------------------------

I'm also attaching two data sets on population by city or county, that we might have time to analyze in class using Benford's law:
Log10(1+1/i) for first digit i.

2-sample z-test for proportions but paired (dependent) rather than independent

http://www.uvm.edu/~dhowell/methods8/Supplements/Testing%20Dependent%20Proportions.pdf

https://onlinecourses.science.psu.edu/stat504/node/96

http://home.ubalt.edu/ntsbarsh/business-stat/otherapplets/PairedProp.htm

101 Statistical Tests, 3rd Ed. By Gopal K. Kanji, Page 57,
Test 23 The Z-test for correlated proportions

Chapter 13

We will use the following link in class: Java (not Javascript) applet that resamples linear regression; it helps explore/explain the concepts from Chapter 13:
http://www.rossmanchance.com/applets/regcoeff/regcoeff.html

Confidence intervals on the regression line, and prediction intervals for new data points:

Testing for linearity:http://en.wikipedia.org/wiki/Lack-of-fit_sum_of_squares

And Evaluation of three lack of fit tests in linear regression models Journal of Applied Statistics
Volume 30, Issue 6, 2003

If we fit a line and get a good R^2, can we say there's a linear trend to the data?

Not really. We should also fit a quadratic (or power, exponential, etc) and show it's not much better than the mx+b fit.

Why You Shouldn't Conclude "No Effect" from Statistically Insignificant Slopes:http://www.carlislerainey.com/2012/06/16/why-you-shouldnt-conclude-no-effect-from-statistically-insignificant-slopes/
More on Concluding "No Effect":http://www.carlislerainey.com/2012/06/27/more-on-concluding-no-effect/

Two diﬀerent ways to bootstrap a regression model
1. Bootstrap data pairs xi = (ci, yi)
2. Bootstrap the residuals ⇒ xi = (ci, ciβˆ + ˆεi1)

http://compdiag.molgen.mpg.de/ngfn/docs/2003/nov/resampling.pdf

Testing for difference of slopes in two data sets:

http://stats.stackexchange.com/questions/13112/what-is-the-correct-way-to-test-for-significant-differences-between-coefficients
http://onlinelibrary.wiley.com/doi/10.1111/j.1745-9125.1998.tb01268.x/abstract
http://www.jstor.org/discover/10.2307/2782277?uid=3739728&uid=2&uid=4&uid=3739256&sid=21103087143891

Calculus Supplement

See that separate file.

Leemis diagram of distributions:

http://www.math.wm.edu/~leemis/chart/UDR/UDR.html

Decision tree of what distribution to use:

http://pages.stern.nyu.edu/~adamodar/New_Home_Page/StatFile/statdistns.htm

College Math Journal, Vol 31 No 4 September 2000: The Lognormal Distribution
by Brian E Smith and Francis J Merceret
page 259-261

http://classes.soe.ucsc.edu/ams113/Winter03/
classes.soe.ucsc.edu/ams113/Winter03/calc.pdf

http://www.zweigmedia.com/RealWorld/cprob/cprobintro.html

http://cs.gettysburg.edu/~leinbach/DRVTI_Conf/Kellett.PDF

http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2931677/

http://jwilson.coe.uga.edu/EMAT6680Fa06/Sexton/STAT%206070/Web2.html

Activites for Calc-Based Statistics Classes
http://www.mathspace.com/NSF_ProbStat/Teaching_Materials/Primarily_Statistics.htm

Probability Distributions Used in Reliability Engineering
ftp://meftp.umd.edu/RIAC/Probability%20Distributions%20Used%20in%20Reliability%20Engineering%20V4.pdf

Basic Concepts of Probability and Statistics for Reliability Engineering; Ernesto Gutierrez-Miravete

http://www.ewp.rpi.edu/hartford/~ernesto/S2007/SMRE/Notes/Review.pdf

Computer Science Majors

Free books:

http://www.greenteapress.com/thinkstats/thinkstats.pdf, uses Python

http://www.greenteapress.com/thinkbayes/thinkbayes.pdf

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

From Algorithms To z-Scores

An Introduction to Statistical Learning, with Applications in R by James, Witten, Hastie and Tibshirani (Springer, 2013). As of January 5, 2014, the pdf for this book will be available for free, with the consent of the publisher, on the book website.

Not-free books:

Probability and Statistics for Computer Scientists, 2nd edition
Michael Baron
UT Dallas
CRC press

Probability Foundations for Engineers
Joel A. Nachlas
Virginia Tech
CRC press

I asked some professors in our CompSci department what CS majors should get out of Math 360, and here are some of their responses:

FDR: False Discovery Rate
http://en.wikipedia.org/wiki/False_discovery_rate

seminal paper, cited more than 22,000 times:
Y. Benjamini and Y. Hochberg. Controlling the false discovery rate: a practical and powerful approach to
multiple testing. Journal of the Royal Statistical Society: Statistical Methodology 57 (1995), 289-300.

p-values and q-values:
http://www.nonlinear.com/support/progenesis/samespots/faq/pq-values.aspx
-------------------------------------
I think it would be helpful if CS students knew about density/distribution functions, perhaps with more emphasis on discrete (but not entirely).
Conditional probability , Bayes rule , joint densities.

Possible Projects:
Diagnosis: medical, mechanical, really anything. Use Naive Bayesian Inference
Classification: Naive Bayesian Inference with MAP estimator - spam/textual filter classifier
Simulation: Monte Carlo techniques, various types of Markov processes
Hypothesis Testing - did this type of user interface increase productivity, did that new protocol increase through-put, etc.
----------------------------
In some cases, it is a bit hard to deconvolute the stats from the science.

Recommender systems has gone the way of matrix decompositions, but understanding distributions is definitely important. Variance, standard deviation, covariance... different forms of correlation, mutual information. Also, ways of looking at error of prediction

Bioinformatics is a bit different, since it is a bit more experimental. you see a lot of use of Fisher's exact test for testing "enrichment" of annotations --- e.g., does a set of n genes found experimentally include more members who are annotated to appear in the nucleus than you would expect by chance? Understanding p-values, q-values/FDR is important.

Bayes rule shows up in several settings.

-----------------------------
Personally, I would think that some Bayesian inference could be useful. Maybe signal detection theory. Cluster analysis might fit MATH 360. You would find a lot of potential projects in artificial intelligence, pattern recognition, and machine learning, among other areas.

Signal detection theory:
http://psych.hanover.edu/JavaTest/STD/
http://wise.cgu.edu/sdtmod/
http://en.wikipedia.org/wiki/Detection_theory
http://www.cns.nyu.edu/~david/handouts/sdt/sdt.html

Review

Try to make a summary table with these column headings:

Row#	#samples : 1, 2, >=3	means or proportions	paired or not	# tails	CI or HT?	Excel function
1
2

The following web site shows you a bunch of statistics scenarios and you click on the statistical technique that is most appropriate, and get instant feedback. There's one type of test we haven't talked about, though: ANOVA. When clicking on types of tests to include, don't click on ANOVA.

http://www-personal.umich.edu/~hamms/spotlight/nts2.html

PS: if you're curious about ANOVA:
" In its simplest form, ANOVA provides a statistical test of whether or not the means of several groups are all equal, and therefore generalizes t-test to more than two groups."
http://en.wikipedia.org/wiki/Analysis_of_variance

See the scanned pages with a lot of good questions, most of which are concept-based. Some notes:
* Only work on the ones that are multiple-choice; the ones labeled "Investigation" are not part of the practice test.
* There are occasional problems that require you to do some statistical calculations, including using z, t, or chi-squared tables or Excel functions.
* on page 621 of the scanned pages, you may skip problem C6 (a six-sided die)
* on page 663 of the scanned pages, you may skip problem C1.

The concept test that we did via emu-online, on confidence intervals and hypothesis tests, is also very good for you to study from.

However, the actual test questions will not be simple alterations of these questions; they will be new contexts.

The test will also include a few computational questions; here are some practice problems for those:

A poll of 1000 people found that 53% said they were Republican and 47% said Democrat (we are ignoring unaffiliated voters). Of the Republicans, 20% were in favor of a particular new political proposal. Of the Democrats, 18% were in favor. Do an appropriate statistical analysis; show all work and reasoning.

In planning for a wind turbine to generate electric power, a city put up a wind-speed sensor in Location A and collected 7 days of data, with resulting speeds (avg per day, in mph) of:
10 12 11 12 9 9 12
The sensor was then moved to Location B, whose measurements were then
9 11 13 12 12 9 8
Do an appropriate statistical analysis; show all work and reasoning. If you need to make any assumptions, write down what you are assuming.

Chapter XKCD

Null Hypothesis:
http://xkcd.com/892/

Multiple Testing: http://xkcd.com/882/

Frequentist vs Bayesian: http://xkcd.com/1132/

Statistically Significant outlier http://www.xkcd.org/539/

Cell Phones and Cancer: http://www.xkcd.org/925/

Placebo blocker: http://xkcd.com/1526/

Trouble for Science: http://xkcd.com/1574/